温位の初期分布
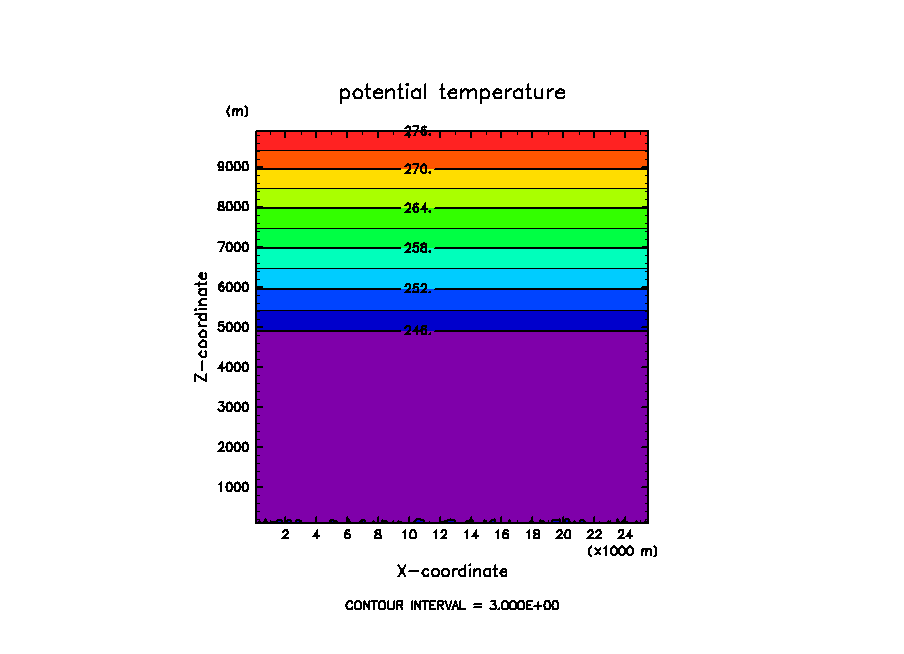
arare-odaka1998-dx200-20051008-PotTempInit.png
温位の水平平均値の時間変化
温位変化の寄与
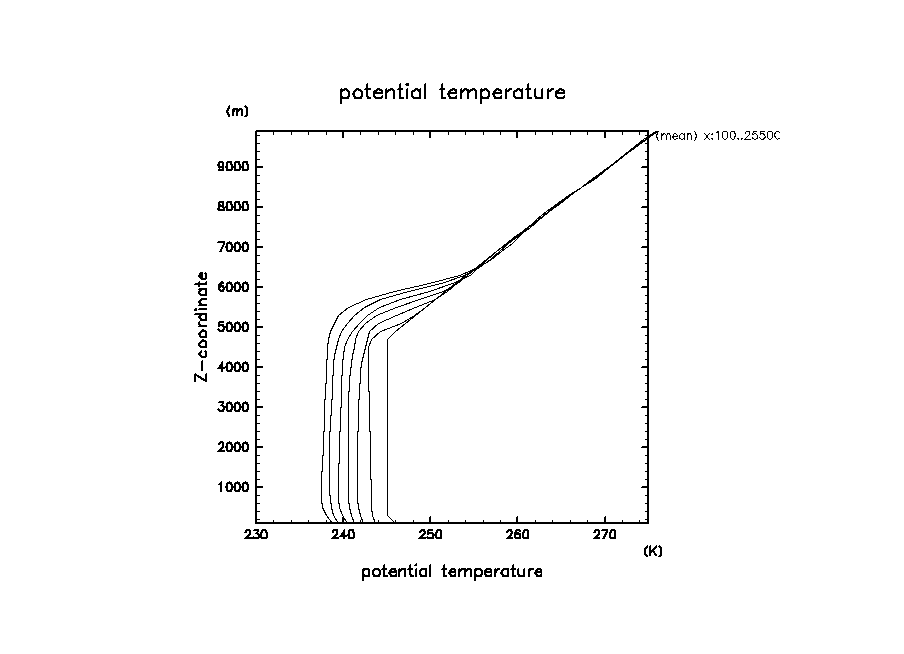
arare-odaka1998-dx200-20051008-PotTempProf.png
右から t = 0, 1, 2, 3, 4, 5, 6 hr
右から t = 0, 1, 2, 3, 4, 5, 6 hr
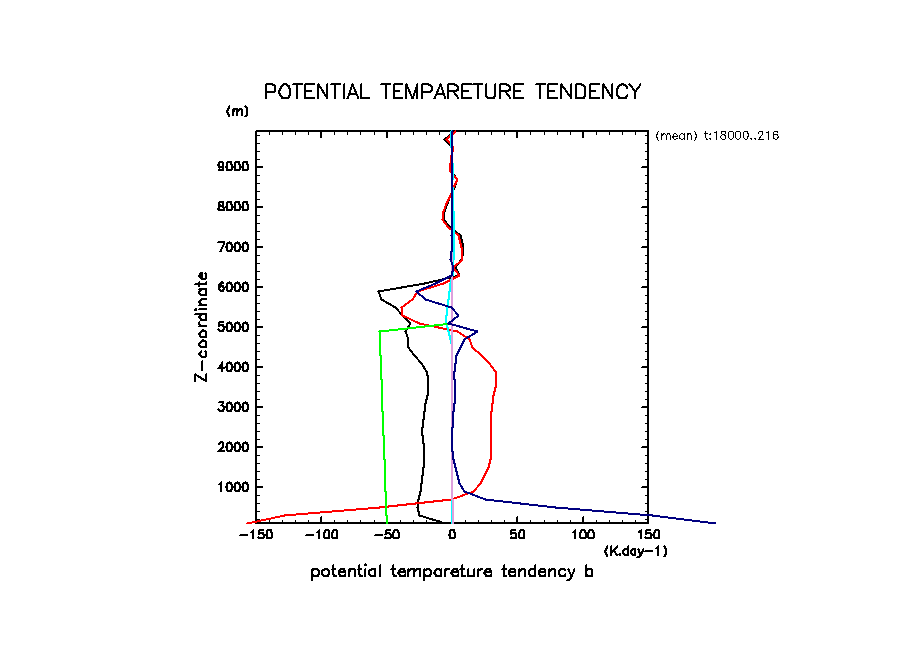
arare-odaka1998-dx200-20051008-PotTempTend.png
t = 5--6 hr の平均. 黒: 合計, 赤: 移流, 青: 拡散, 緑: 放射, 水色: 散逸
t = 5--6 hr の平均. 黒: 合計, 赤: 移流, 青: 拡散, 緑: 放射, 水色: 散逸
温位(水平平均からのずれ)

arare-odaka1998-dx200-20051008-PotTemp-t0.png
t = 0
t = 0

arare-odaka1998-dx200-20051008-PotTemp-t7200.png
t = 2 hr
t = 2 hr
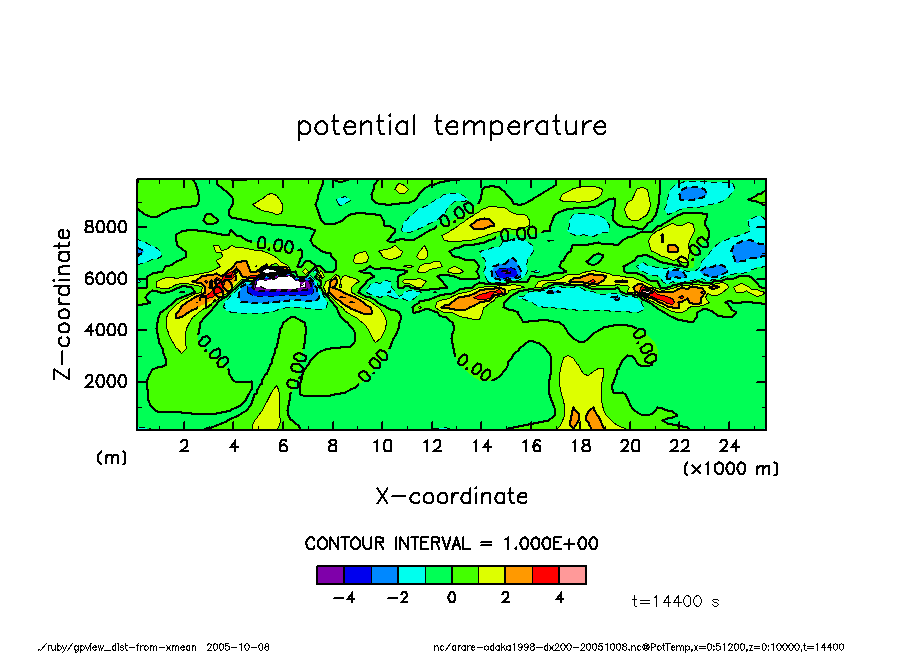
arare-odaka1998-dx200-20051008-PotTemp-t14400.png
t = 4 hr
t = 4 hr
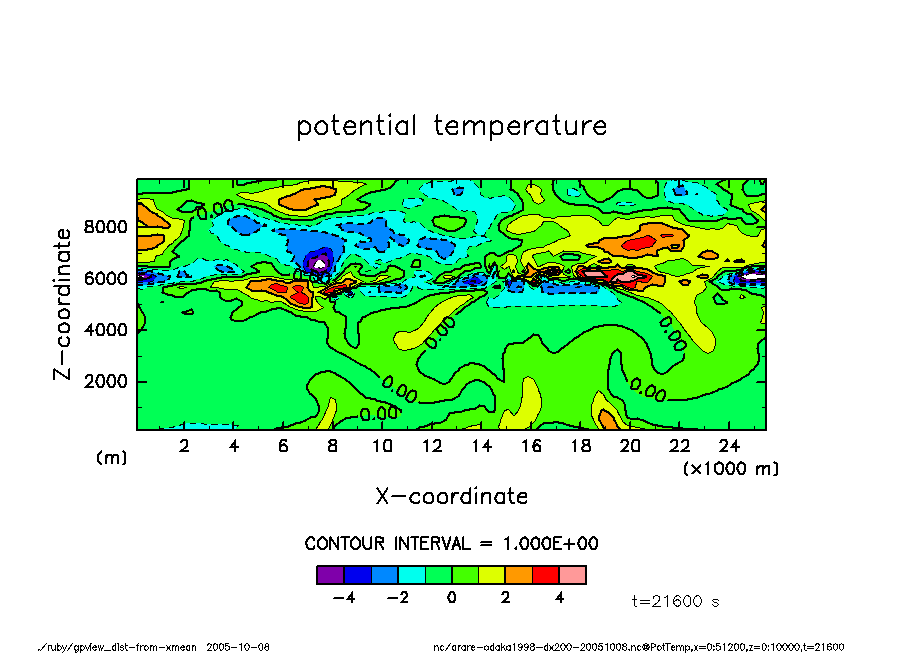
arare-odaka1998-dx200-20051008-PotTemp-t21600.png
t = 6 hr
t = 6 hr
水平速度

arare-odaka1998-dx200-20051008-VelX-t0.png
t = 0
t = 0

arare-odaka1998-dx200-20051008-VelX-t7200.png
t = 2 hr
t = 2 hr
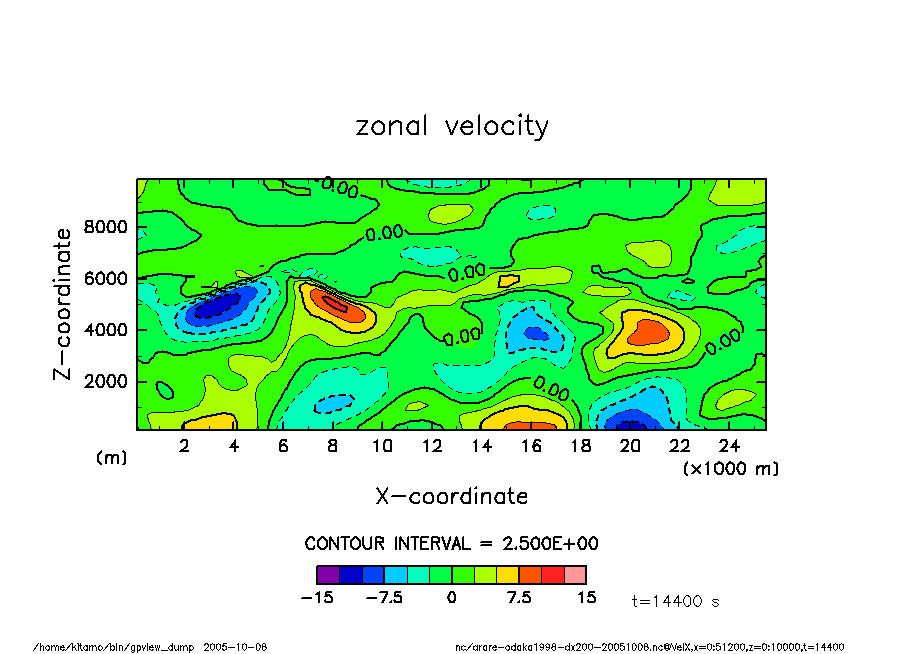
arare-odaka1998-dx200-20051008-VelX-t14400.png
t = 4 hr
t = 4 hr
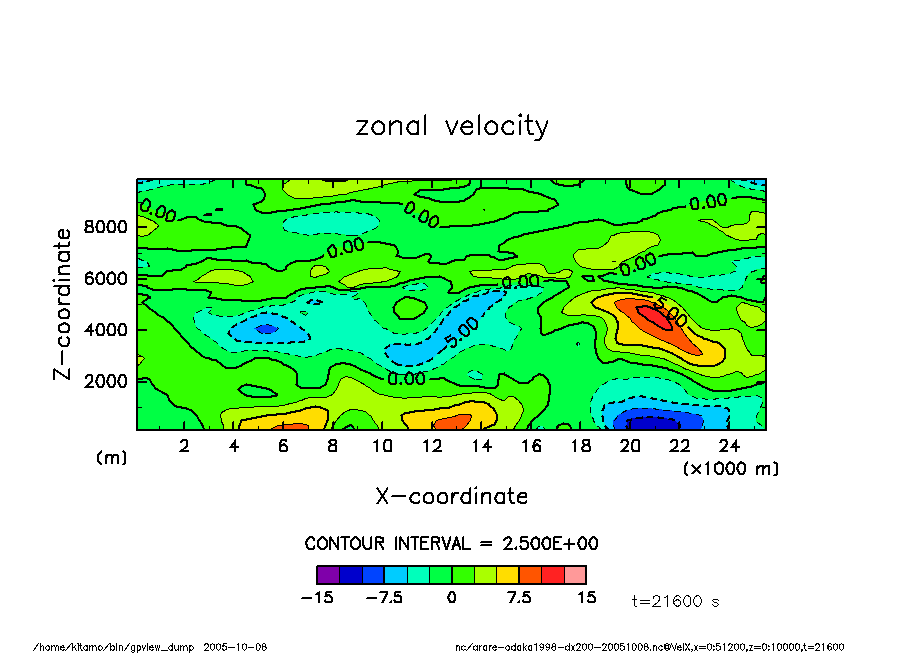
arare-odaka1998-dx200-20051008-VelX-t21600.png
t = 6 hr
t = 6 hr
鉛直速度

arare-odaka1998-dx200-20051008-VelZ-t0.png
t = 0
t = 0

arare-odaka1998-dx200-20051008-VelZ-t7200.png
t = 2 hr
t = 2 hr
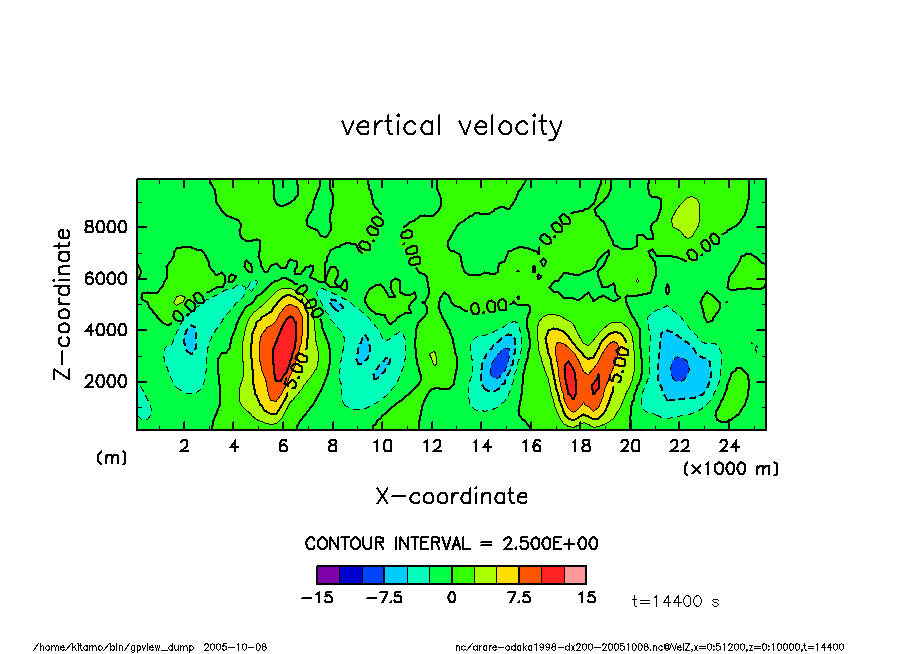
arare-odaka1998-dx200-20051008-VelZ-t14400.png
t = 4 hr
t = 4 hr

arare-odaka1998-dx200-20051008-VelZ-t21600.png
t = 6 hr
t = 6 hr
乱流拡散係数(熱)
arare-odaka1998-dx200-20051008-Kh-t0.png
t = 0
t = 0

arare-odaka1998-dx200-20051008-Kh-t7200.png
t = 2 hr
t = 2 hr

arare-odaka1998-dx200-20051008-Kh-t14400.png
t = 4 hr
t = 4 hr

arare-odaka1998-dx200-20051008-Kh-t21600.png
t = 6 hr
t = 6 hr
乱流拡散係数(運動量)

arare-odaka1998-dx200-20051008-Km-t0.png
t = 0
t = 0

arare-odaka1998-dx200-20051008-Km-t7200.png
t = 2 hr
t = 2 hr
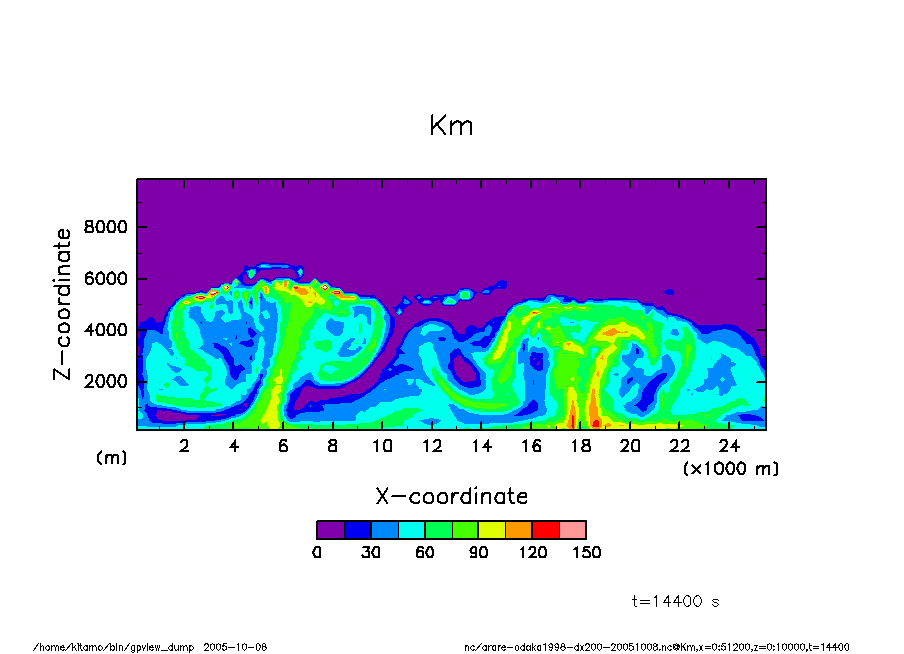
arare-odaka1998-dx200-20051008-Km-t14400.png
t = 4 hr
t = 4 hr
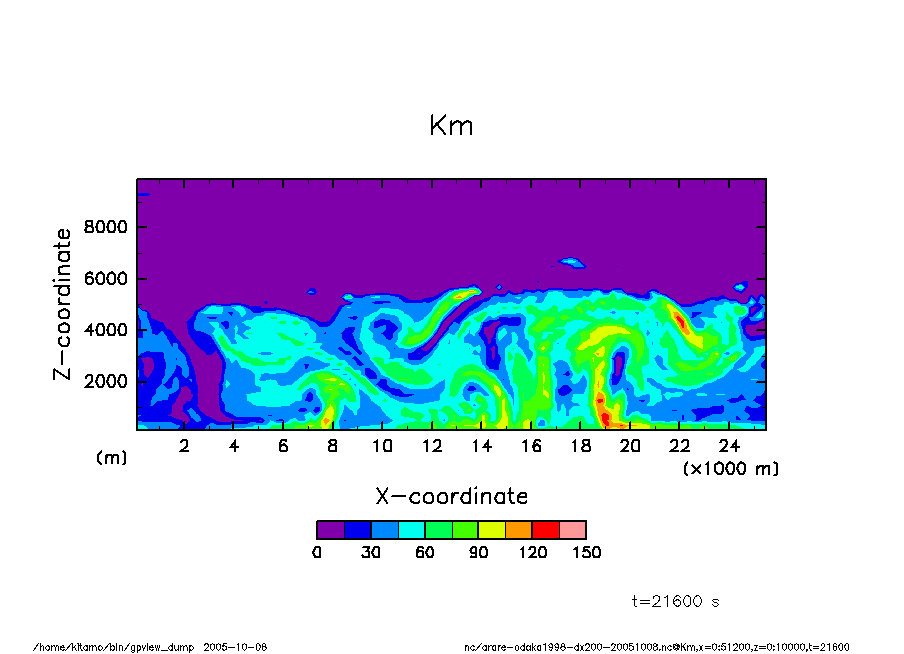
arare-odaka1998-dx200-20051008-Km-t21600.png
t = 6 hr
t = 6 hr
全質量

arare-odaka1998-dx200-20051008-MassTotal.png
t = 0 を 1 とした時の値をプロットしている.
t = 0 を 1 とした時の値をプロットしている.
全運動エネルギー
全静的エネルギー
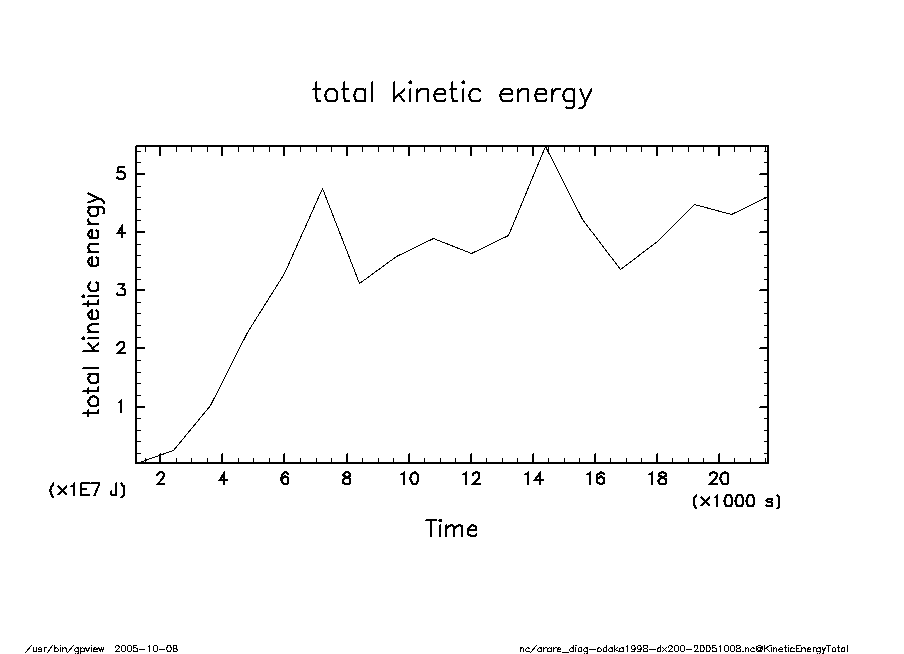
arare-odaka1998-dx200-20051008-KineticEnergyTotal.png

arare-odaka1998-dx200-20051008-PotentialEnergyTotal.png