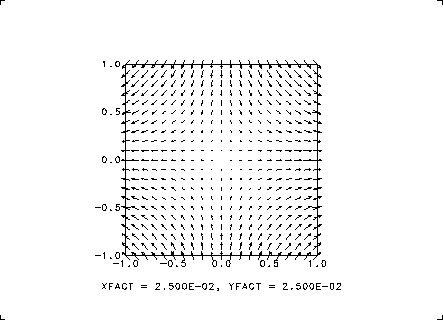
今度は, 2次元のベクトル場を手早く矢印で見たいというときの例題です. 次
の quick5 は簡単な変形場を描くプログラムですが, GRPH2 の UGPACK
にあるメソッド(元サブルーチン) ugvect 1つを呼ぶだけで十分です. 前節の等高線
図の場合と同様に, おまかせの座標軸を描画したあとで ugvect ルーチ
ンを呼んでベクトル場を描いています.
この例では, やはり, 等間隔の格子点を設定して, それぞれの格子点でのベク
トルを矢印で表現します. おまかせ描画のときには, ベクトルの長さが格子点
間隔を越えないようにスケーリングファクターが決定され, それを乗じてベク
トルが描かれます. この場合, x成分とy成分のスケーリングファクターは
同じになっていて, 図の下部マージンにはその値が表示されています.
ベクトル場も UGPACK のルーチンを使うことによって高度な作図ができるよ うになります. これも第10章で説明することにしましょう.
# quick5.rb
require "narray"
require "numru/dcl"
include NumRu
include Math
nx = 21
ny = 21
xmin = -1.0
xmax = 1.0
ymin = -1.0
ymax = 1.0
u = NArray.sfloat(nx, ny)
v = NArray.sfloat(nx, ny)
#-- data ----
for j in 0..ny-1
for i in 0..nx-1
x = xmin + (xmax-xmin)*i/(nx-1)
y = ymin + (ymax-ymin)*j/(ny-1)
u[i,j] = x
v[i,j] = -y
end
end
#-- graph ----
iws = (ARGV[0] || (puts ' WORKSTATION ID (I) ? ;'; DCL::sgpwsn; gets)).to_i
DCL::gropn iws
DCL::grfrm
DCL::grswnd(xmin, xmax, ymin, ymax)
DCL::grsvpt(0.2, 0.8, 0.2, 0.8)
DCL::grstrn(1)
DCL::grstrf
DCL::usdaxs
DCL::ugvect(u, v)
DCL::grcls
PROGRAM QUICK5

計算機のなまり 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||