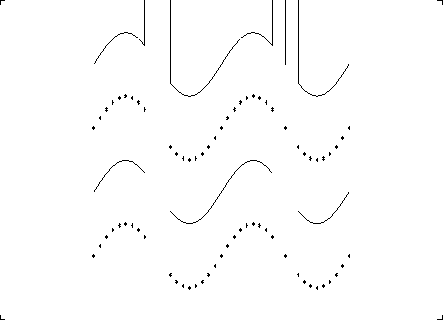
miss1.rb: frame1
データの中に欠損がある場合には, MATH1 の SYSLIB メソッド(元サブルーチン)パッケージ にある gllset ルーチンで欠損値処理の指定に関する内部変数 'LMISS' を .true. にして, 欠損値処理を有効にします. 欠損値処理 の制御は SGPACK だけでなく DCL 全体で統一的に行われるために, 欠損値処 理に関する内部変数の管理はsgpget/sgpset ではなく glpget/glpset で行われています(p は i, r, l または c).
このように指定すると, データの値が999.であるものは欠損値と見なして, こ
れから見るような欠損値処理を行ないます. 欠損値999.が実際のデータ範囲に
入っていて, 別の値にしたい場合には, glrset ルーチンによって実数
の欠損値をあらわす内部変数 'RMISS' を変更します.
まず, miss1プログラムを例に, ポリラインとポリマーカーのプリミティ ブで欠損値処理がどのように行なわれるか見てみましょう. 第3 章で用いた正弦メソッド(元関数)のデータに欠損値 999.を埋め込みます. データの1/4のと ころでは3点連続して欠損値とし, 3/4のところでは, 有効な点が欠損値データ に挟まれて1点だけ孤立しているように与えます.
# miss1.rb
require "narray"
require "numru/dcl"
include NumRu
include NMath
nmax = 40
xmin = 0.0
xmax = 4*PI
ymin = -1.0
ymax = 1.0
x = NArray.sfloat(nmax+1)
y = NArray.sfloat(nmax+1)
#-- data ----
dt = xmax/nmax
x = x.indgen * dt
y = sin(x)
n1 = nmax/4
rmiss = DCL::glrget('RMISS')
y[n1-1] = rmiss
y[n1] = rmiss
y[n1+1] = rmiss
n2 = n1*3
y[n2-1] = rmiss
y[n2+1] = rmiss
#-- graph ----
iws = (ARGV[0] || (puts ' WORKSTATION ID (I) ? ;'; DCL::sgpwsn; gets)).to_i
DCL::sgopn iws
DCL::grfrm
#-- default ----
DCL::grswnd(xmin, xmax, ymin, ymax)
DCL::grsvpt( 0.1, 0.9, 0.7, 0.9)
DCL::grstrn(1)
DCL::grstrf
DCL::sgplu(x, y)
DCL::grswnd(xmin, xmax, ymin, ymax)
DCL::grsvpt( 0.1, 0.9, 0.5, 0.7)
DCL::grstrn(1)
DCL::grstrf
DCL::sgspmt(3)
DCL::sgpmu(x, y)
#-- cover loss data ----
DCL::gllset('LMISS', true)
DCL::grswnd(xmin, xmax, ymin, ymax)
DCL::grsvpt( 0.1, 0.9, 0.3, 0.5)
DCL::grstrn(1)
DCL::grstrf
DCL::sgplu(x, y)
DCL::grswnd(xmin, xmax, ymin, ymax)
DCL::grsvpt( 0.1, 0.9, 0.1, 0.3)
DCL::grstrn(1)
DCL::grstrf
DCL::sgpmu(x, y)
DCL::grcls
program miss1

欠損値処理をしない(デフォルト)で sgplu と sgpmu のルーチン
を呼んだ結果が上の2つです. 他のデータと比べて999.は非常に大きな値です
から, ポリラインではほぼ真上に線を引いて最大作画範囲を飛び出しています.
また, ポリマーカーでもこれらの点は作画範囲を飛び出してしまって描かれま
せん.
gllset ルーチンで内部変数 'LMISS' を .true. にして, 欠損値処理を行なって描いた結果が下の2つです. ポリラインでは欠損値の前 後を線で結びません. 有効な点が1点だけ孤立している場合には, その点を結 ぶことができないので, そこには何も描かれません. また, ポリマーカーでは 欠損値の点にはマーカーを打ちません. この例では, ポリマーカーの結果はど ちらも同じですが, 欠損値を小さくして2.とすると違いは明らかです.