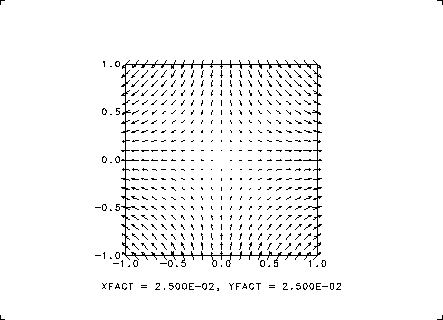
今度は, 2次元のベクトル場を手早く矢印で見たいというときの例題です. 次
の QUICK5 は簡単な変形場を描くプログラムですが, GRPH2 の UGPACK
にあるサブルーチン UGVECT 1つを呼ぶだけで十分です. 前節の等高線
図の場合と同様に, おまかせの座標軸を描画したあとで UGVECT ルーチ
ンを呼んでベクトル場を描いています.
この例では, やはり, 等間隔の格子点を設定して, それぞれの格子点でのベク
トルを矢印で表現します. おまかせ描画のときには, ベクトルの長さが格子点
間隔を越えないようにスケーリングファクターが決定され, それを乗じてベク
トルが描かれます. この場合, x成分とy成分のスケーリングファクターは
同じになっていて, 図の下部マージンにはその値が表示されています.
ベクトル場も UGPACK のルーチンを使うことによって高度な作図ができるよ うになります. これも第10章で説明することにしましょう.
PROGRAM QUICK5
PARAMETER ( NX=21, NY=21 )
PARAMETER ( XMIN=-1, XMAX=1, YMIN=-1, YMAX=1 )
REAL U(NX,NY), V(NX,NY)
*-- 2次元ベクトルデータ: 変形場 ----
DO 20 J=1,NY
DO 10 I=1,NX
X = XMIN + (XMAX-XMIN)*(I-1)/(NX-1)
Y = YMIN + (YMAX-YMIN)*(J-1)/(NY-1)
U(I,J) = X
V(I,J) = -Y
10 CONTINUE
20 CONTINUE
*-- グラフ ----
WRITE(*,*) ' WORKSTATION ID (I) ? ;'
CALL SGPWSN
READ (*,*) IWS
CALL GROPN( IWS )
CALL GRFRM
CALL GRSWND( XMIN, XMAX, YMIN, YMAX )
CALL GRSVPT( 0.2, 0.8, 0.2, 0.8 )
CALL GRSTRN( 1 )
CALL GRSTRF
CALL USDAXS
CALL UGVECT( U, NX, V, NX, NX, NY )
CALL GRCLS
END
PROGRAM QUICK5

計算機のなまり 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||