/地球流体セミナー
/講演資料一覧
/2002-08-26/
MSTRN8 を用いた一次元放射対流平衡
〜暴走温室限界の計算〜
はしもとじょーじ(東大・気候システム)
2002 年 8 月 26 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
目次
|

|
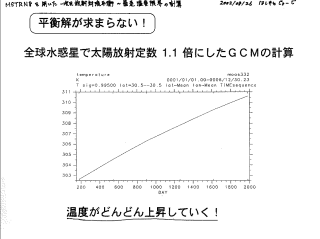
平衡解が求まらない → 暴走温室効果?
- 暴走温室効果
…温室効果によって温度が際限無く上昇.
問題意識: 暴走温室はどこで始まるのか?
- 放射コードの性質によって決まる
- 一次元放射対流平衡モデルで調べる
|

|
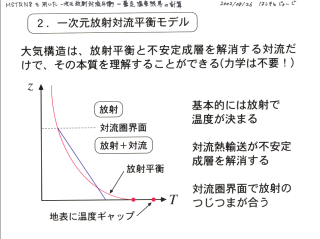
一次元放射対流平衡モデルの問題点と対応策
- 雲量が計算できない
… 地面のアルベドを変える
- 水蒸気の存在量が計算できない
… 対流圏は相対湿度一定, 成層圏は圏界面の混合比で一定
- 対流層の温度勾配
… 段熱温度勾配 or なんらかの勾配を仮定
|

|
モデル(MSTRN8) の計算手順
- 放射コードは CCSR/NIES AGCM に組み込まれているものを用いる
|

|
コントロール実験: 現在の地球条件
(相対湿度 0.5, 地面アルベド 0.27)
US 標準大気 (1976, 中緯度) と比べると…
- 圏界面温度が低い: 成層圏の水蒸気量が大きい
- 上部対流圏の温度勾配が大きい: 相対湿度を固定したため.
現実では対流圏下層で 0.8, 上層では 0.2-0.3.
|
|
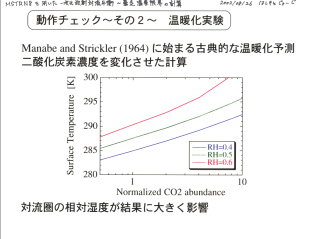
コントロール実験: 温暖化実験
Manabe & Strickler (1964) の再現実験
- CO2 倍増で 2 K 程度昇温
- 水蒸気の相対湿度の感度大
|
|
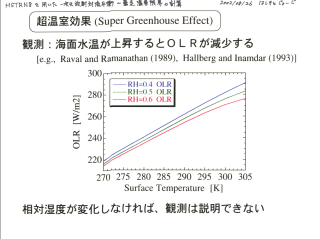
超温室効果の実験:
地表温度を与えて OLR を計算する.
- 地表温度に比例して OLR も増大する. 観測とは矛盾する結果.
|

|
暴走温室効果の定義とメカニズム
- 暴走温室状態 … 平衡状態で海洋が存在しない(温度が上昇し続ける).
- 暴走温室効果 … 大気が射出できる放射には限界がある.
限界を越えたエネルギーが入射すると, 温度が上がり続ける.
- 良くある誤解 … 力学的な不安定のこと.
|
|
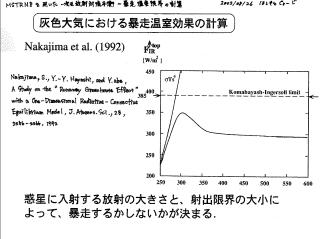
灰色大気の暴走温室計算 (Nakajima, et al., 1992)
|

|
射出限界の分類と存在理由
- 成層圏が規定する限界 (Komabayashi-Ingersoll 限界):
- 圏界面の温度によって決まる圏界面水蒸気量
- 大気上端の射出量と放射平衡から決まる圏界面水蒸気量
両者が一致する所が射出限界となる.
- 温度勾配が規定する限界 (Nakajima et al., 1992):
|
|
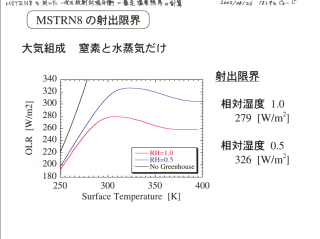
MSTRN8 の射出限界
大気組成は窒素, 水蒸気のみ
- 射出限界は灰色大気の場合にくらべ小さくなる.
- 観測される全球平均 OLR は 240 W/m2
- 熱帯の平均 OLR は相対湿度 1.0 の場合の射出限界に近い
|
|
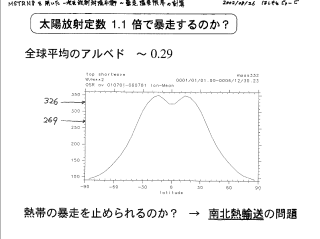
暴走するかしないか?
太陽定数 1.1 倍, アルベド 0.29 の場合の入射太陽放射フラックス
- 熱帯は射出限界を超えている, 極域は射出限界以下.
- 全球で暴走状態になるかどうかは南北熱輸送能力が決める.
|
|
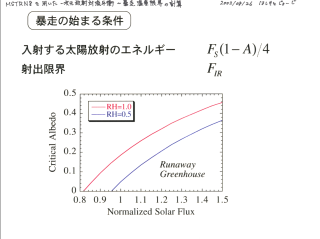
暴走の始まる条件
入射太陽放射 > 射出限界 なら暴走.
- 現在の地球条件では暴走しない
- 現在の金星条件でも暴走しない
|

|
Nakajima, et al. (1992) の計算結果
灰色大気における射出限界
|
|
|
参考文献
- Hallberg, R., and A. Inamdar, 1993:
Observations of seasonal variations in atmospheric greenhouse trapping and
its enhancement at high sea surface temperature.
J. Climate, 6, 2049-2062.
- Ingersoll, A. P., 1969:
The runaway greenhouse: A history of water on Venus.
J. Atmos. Sci., 26, 1191-1198.
- Komabayashi, M., 1967:
Discrete equilibrium temperatures of a hypothetical planet with the
atmosphere and the hydrosphere of one component-two phase system under
constant solar radiation.
J. Meteor. Soc. Japan, 45, 137-139.
- Komabayashi, M., 1968:
Conditions for the coexistence of the atmosphere and the oceans.
Shizen, 23, No. 2, 24-31 (in Japanese).
- Manabe, S., and R. F. Strickler, 1964:
Thermal equilibrium of the atmosphere with a convective adjustment.
J. Atmos. Sci., 21, 361-385.
- Nakajima, S., Y.-Y. Hayashi and Y. Abe, 1992:
A study on the 'runaway greenhouse effect' with a one-dimensional
radiative-convective equilibrium model.
J. Atmos. Sci., 49, 2256-2266.
- Raval, A. and V. Ramanathan, 1989:
Observational determination of the greenhouse effect.
Nature, 342, 758-761.
- Nakajima, T., M. Tsukamoto, Y. Tsushima, A. Numaguti, and T. Kimura, 2000:
Modeling of the radiative process in an atmospheric general circulation model.
Appl. Opt., 39, 4869-4878.
|
Odaka Masatsugu & Sasaki Youhei
2002-09-09
|