/地球流体セミナー
/講演資料一覧
/2003-03-17/
中緯度大気変動の力学 −中立モードを中心に−
渡部雅浩氏(北大・地球環境)
2003 年 3 月 17 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|

|
中高緯度大気の長周期変動
|
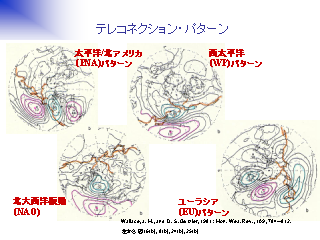
図は Wallace, and Gutzler, 1981
|
テレコネクションパターン
- 冬の 12 月月平均 500 hPa 等圧面高度の一点相関図:
図中の赤点で示した地点と他の地点との相関
- 冬の北半球に特徴的な気圧場のパターンをはじめて示した
|

|
熱帯域のテレコネクション
|

|
PNA パターンとエルニーニョ
- 熱帯の大気強制に対する応答として解釈
- エルニーニョの場合の大気場の観測結果に基づく
|
|
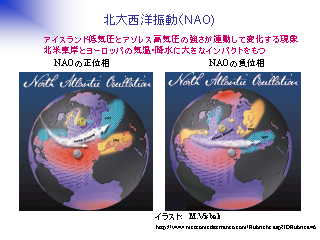
北大西洋振動 (NAO)
|
|
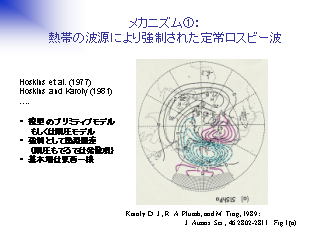
メカニズム1: 熱帯の熱源により強制された定常ロスビー波
線形プリミティブモデルの強制に対する応答として考える
- 熱源を与えて大気の応答を見る
- 基本場の風速は観測された東西平均値を与える
- 定常ロスビー波の伝播の様子はテレコネクションパターンによく似ている
|

|
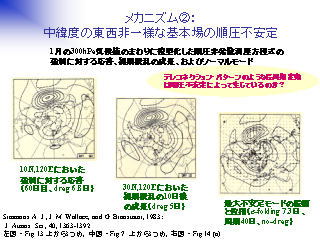
メカニズム1: 中緯度の東西非一様な基本場からのエネルギー変換
基本場の風速が東西一様でない場合: 基本場の風は北半球の 1 月
- 観測値から抜きだした剛体回転場: 南北対称な応答が現れる
- 東西一様場: 同じ緯度に熱源を与えると経度によらず同じ応答が現れる
(アタリマエ)
- 東西非一様場: 基本場は東西非一様だが,
同じ緯度に熱源を与えると経度によらず同じ応答 (地理的に同じ位置に同じパターン)が現れる (なぜだろう?)
- ずらす経度幅の程度による. インド洋から中部太平洋の範囲では同じ.
|
|
メカニズム2: 中緯度の東西非一様な基本場の順圧不安定
- あまりうまくない: 現実的な摩擦を与えた場合, 実効的な成長率が小さい
- 結果的には中立モードによる理解と同じ見方 ?
|
|
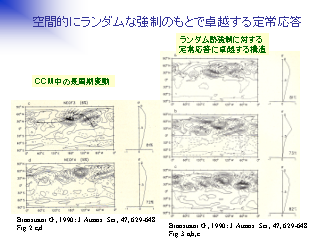
空間的にランダムな強制のもとで卓越する定常応答
(左)大気大循環モデルの結果 (EOF3, EOF4)
(右)線形定常プリミティブモデルの結果
- 300 hPa 等圧面高度 (北半球冬)
- 空間的にランダムな分布の強制を与え線形応答問題を解く.
200 の異なる初期値に対する結果を平均
- 強制源の空間パターンに規則性がなくても,
大気の気圧パターンにはある特徴的な構造が応答として現れる.
|

|
まとめ・疑問点・問題点など
- 観測値から得られた特徴的な気圧パターン (EOF) に,
なんらかの力学的解釈を与えれないだろうか?
- EOF は線形大気モデルの固有関数に対応するのか?
|

|
中立モードの理論
- Dymnikov (1988) がさきがけ
- 西側の科学者では Navarra (1993)
|

|
中立モードの理論 1-1
- Ψ の平均場は適当な強制によって維持されると考える.
|

|
中立モードの理論 1-2
|

|
中立モードの理論 1-3
- Ψ の斉次解部分を固有振動数と固有ベクトルで表現できると仮定
|
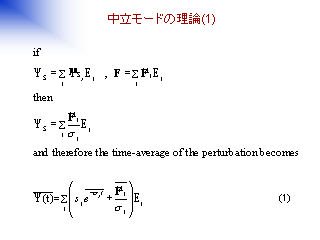
|
中立モードの理論 1-4
|

|
中立モードの理論 1-5
|

|
中立モードの理論 2-1: 特異ベクトル
- 観測データから抽出されたパターン (ex. EOF) をどうとらえるか?
- 与えられた力学系の係数行列の固有ベクトルが直交しない場合,
その他のなんらかの直交ベクトルで理解できないか, を考える.
|

|
中立モードの理論 2-2
|

|
中立モードの理論 2-3
|

|
中立モードの理論 2-4
|

|
中立モードの理論 2-5
|
|
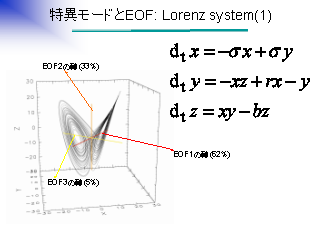
特異モードと EOF: Lorenz system (1)
|

|
特異モードと EOF: Lorenz system (2)
|
|
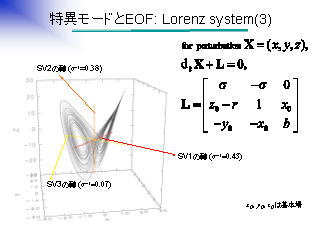
特異モードと EOF: Lorenz system (3)
|
|
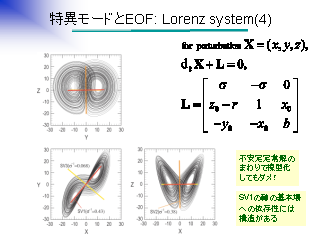
特異モードと EOF: Lorenz system (4)
|
|
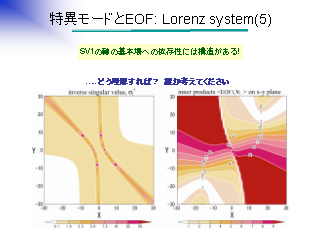
特異モードと EOF: Lorenz system (5)
|
|
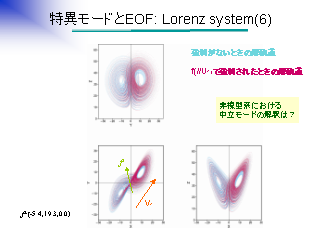
特異モードと EOF: Lorenz system (6)
|

|
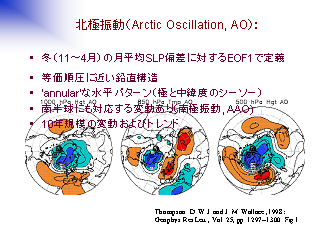
中立モードの計算例その 1: 北極振動
|
|
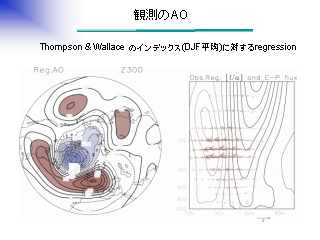
北極振動 (AO) とは ?
|

|
AO のメカニズムについて
|
|
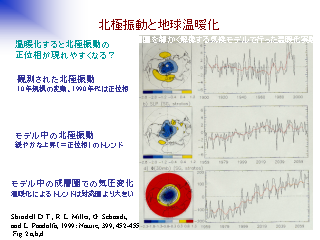
北極振動と地球温暖化
|
|
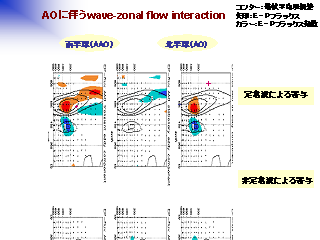
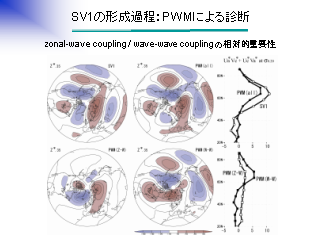
AO にともなう波動平均流相互作用
- 月より長い周期と短い周期の波による平均東西風の加速寄与
- 月より長い周期の波の寄与が大きい
|
|
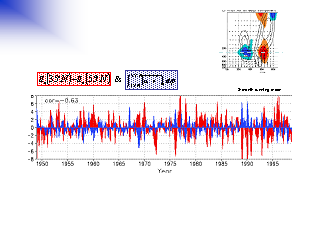
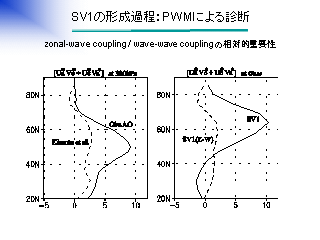
南向き運動量輸送と平均風速偏差の南北差との関係
- 南向きの運動量輸送 (青) と平均風速偏差の南北差 (赤) によい相関がある.
|
|
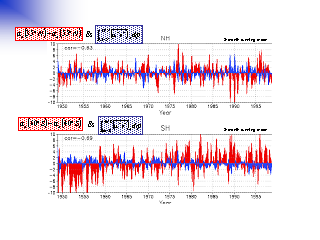
南北の運動量輸送と平均風速偏差の南北差との関係
|

|
AO の力学的起源を調べるための戦略
|

|
線形傾圧モデル
|

|
モデル方程式
|
|
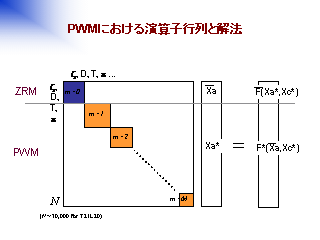
PWM における演算子行列と解法
|
|
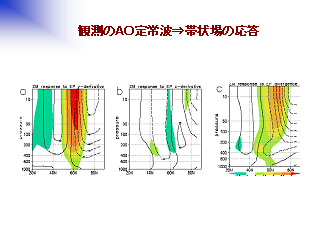
観測の AO 定常波と帯状場の応答 (北半球東西平均場)
|
|
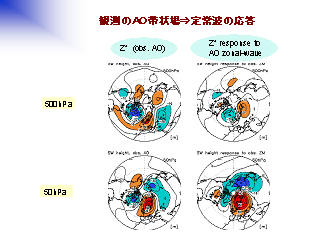
観測の AO 定常波と帯状場の応答 (北半球)
|

|
SVD の前に (1)
|

|
SVD の前に (2)
|
|
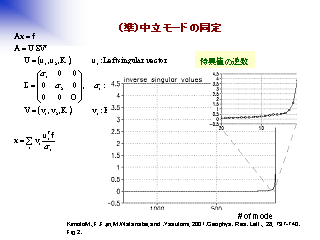
中立モードの同定
|
|
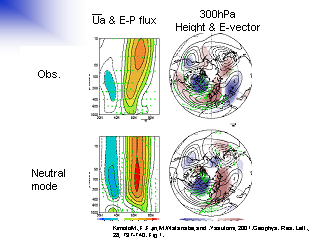
中立モードと観測結果との比較
|
|
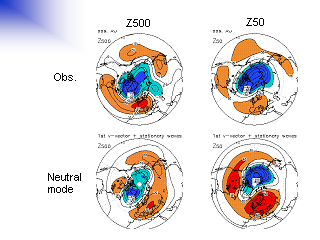
観測される AO と中立モードの水平構造の比較
|
|
観測される AO
|
|
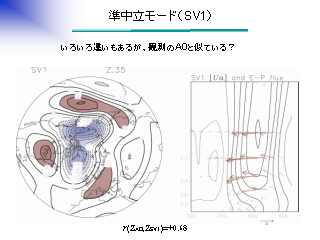
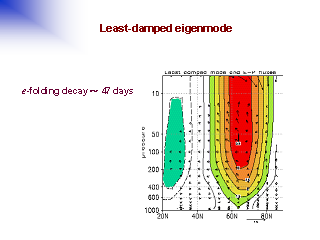
準中立モード
|
|
準中立モードの子午面構造
|
|
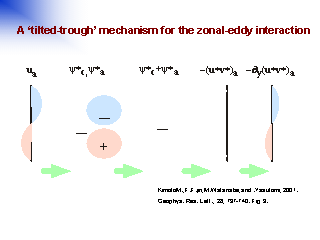
波による加速機構
- 平均風のシアーによって波の位相が傾き, 平均風シアーを強める
|
|
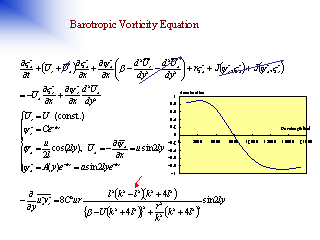
順圧渦度方程式
|

|
まとめ
- 線形のプリミティブモデルにおける特異値分解から,
AO に近い波のパターンを得ることができる
- 力学的には AO は NAO とは独立であると判断できる?
|

|
モード計算に含まれなかったもの
|
|
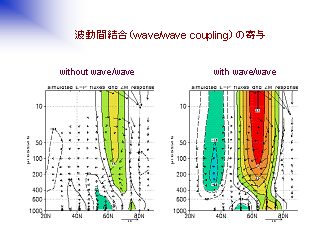
波動間結合の寄与
|
|
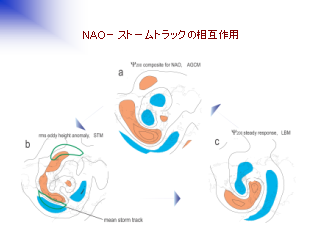
NAO とストームトラックの相互作用
|
|
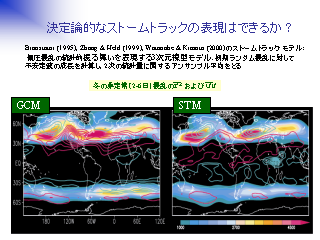
決定論的なストームトラックの表現はできるか?
|

|
中立モード計算その 2: 3 次元基本場のもとでのモード
|

|
ここまでの結果
|
|
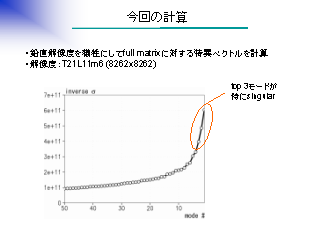
今回の計算
|
|
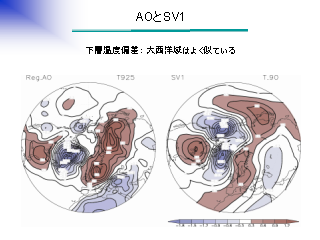
AO と SV1
|
|
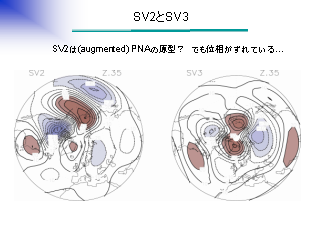
SV2 と SV3
|
|
SV1 の形成過程: PWM による診断 (1)
|
|
SV1 の形成過程: PWM による診断 (2)
|
|
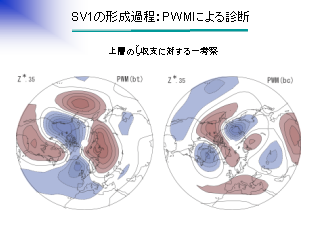
SV1 の形成過程: PWM による診断 (3)
|
|
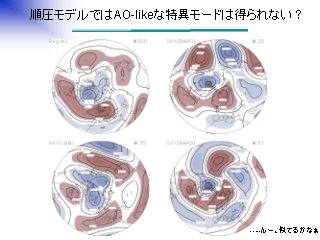
順圧モデルでは AO-like な特異モードは得られない?
|
|
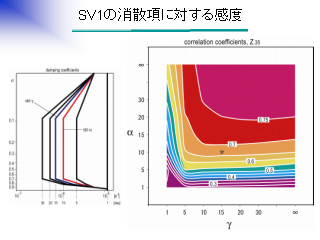
SV1 の消散項に対する感度
|
|
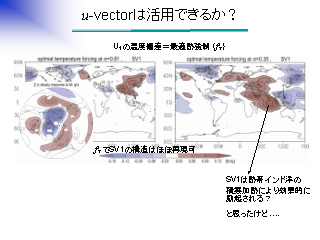
u-vector は活用できるか? (1)
|
|
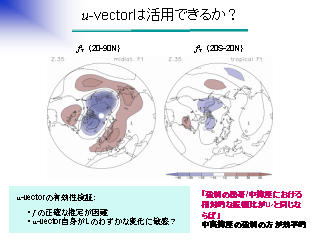
u-vector は活用できるか? (2)
|
|
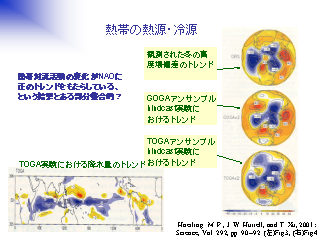
熱帯の熱源・冷源
|
|
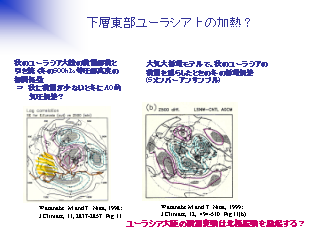
下層東部ユーラシア上の加熱?
|

|
まとめ
|
参考文献
-
Ambaum M. H. P., B. J. Hoskins, and D. B. Stephenson, 2001:
Arctic oscillation or north atlantic oscillation?
J. Climate, 14, 3495-3507.
-
Bladé I., 1996:
On the relationship of barotropic singular modes to the low-freq
uency variability of a general circulation model.
J. Atmos. Sci., 53, 2393-2399.
-
Branstator G., 1985a:
Analysis of general circulation model sea-surface temperature anomaly
simulationsusing a linear model. part I: Forced solutions.
J. Atmos. Sci., 42, 2225-2241.
-
Branstator G., 1985b:
Analysis of general circulation model sea-surface temperature anomaly
simulations using a linear model. part II: Eigenanalysis.
J. Atmos. Sci., 42 2242-2254.
-
Branstator G., 1990:
Low-frequency patterns induced by stationary waves.
J. Atmos. Sci., 47, 629-648.
-
G. Branstator., 1995:
Organization of storm track anomalies by recurring
low-frequency circulation anomalies.
J. Atmos. Sci., 52, 207-226.
-
Deser C., 2000:
On the teleconnectivity of the 'arctic oscillation'.
Geophys. Res. Lett., 27, 779-782.
-
DeWeaver E., and S. Nigam, 2000a:
Do stationary waves drive the zonal-mean jet anomalies of the northern
winter?
J. Climate, 13, 2160-2176.
- DeWeaver E., and S. Nigam, 2000:
Zonal-eddy dynamics of the north atlantic oscillation.
J. Climate, 13, 3893-3914.
-
Dymnikov V. P., 1988:
Relationship of natural orthogonal components of the fields of
meteorological characteristics to the eigenfunctions of dynamical
operators.
Izv. Atmos. Oceanic Phys., 24, 493-496.
-
Goodman J., and J. Marshall, 2003:
Using neutral singular vectors to study low-frequency atmospheric
variability.
J. Climate, in press.
-
Horel J. D., and J. M. Wallace, 1981:
Planetary scale atmospheric phenomena associated with the
southern oscillation. Mon. Wea. Rev., 109, 813-829.
-
Hoskins B. J., and D. J. Karoly, 1981:
The steady linear response of a spherical atmosphere to thermal
and orographicalforcing. J. Atmos. Sci., 38, 1179-1196.
-
Hoskins B. J., A. J. Simmons, and D. C. Andrews, 1977:
Energy dispersion in a barotropic atmosphere.
Quart. J. R. Met. Soc., 103, 553-567.
-
Itoh H., 2002:
True versus apparent arctic oscillation.
Geophys. Res. Lett., 29, p. 10.1029/2001GL013978.
-
Itoh H., and M. Kimoto, 1999:
Weather regimes, low-frequency oscillations, and principal patterns of
variability:
A perspective of extratropical low-frequency variability.
J. Atmos. Sci., 56, 2684-2705.
-
Karoly D. J., R. A. Plumb, and M. Ting, 1989:
Examples of the horizontal propagation of quasi-stationary waves.
J. Atmos. Sci., 46 2802-2811.
-
Kimoto M., F. -F. Jin, M. Watanabe, and N. Yasutomi, 2001:
Zonal-eddy coupling and a neutral mode theory for the arctic oscillation.
Geophys. Res. Lett., 28, 737-740.
-
Limpasuvan V., and D. L. Hartmann, 1999:
Eddies and the annular modes of climate variability.
Geophys. Res. Lett., 26, 3133-3136.
-
Marshall, J., and F. Molteni, 1993:
Toward a dynamical understanding of planetary-scale flow regimes.
J. Atmos. Sci., 50, 1792-1818.
-
Metz W., 1994:
Singular modes and low-frequency atmospheric variability.
J. Atmos. Sci., 51 1740-1753.
-
Navarra, A., 1993:
A new set of orthonormal modes for linearized meteorological problems.
J. Atmos. Sci., 50, 2569-2583
-
Nitta T., 1987:
Convective activities in the tropical western pacific and their
impact on the northern hemisphere summer circulation.
J. Meteor. Soc. Japan, 65, 373-390.
-
North G. R.,1984:
Empirical orthogonal functions and normal modes.
J. Atmos. Sci., 41, 879-887.
-
Shindell D. T., R. L. Miller, G. Schmidt, and L. Pandolfo, 1999:
Simulation of recent northern winter climate trends by greenhouse-gas
forcing.
Nature, 399, 452-455.
-
Simmons A. J., J. M. Wallace, and G. Branstator, 1983:
Barotropic wave propagation and instability, and atmospheric
teleconnection patterns.
J. Atmos. Sci., 40, 1363-1392.
-
Thompson D. W. J., and J. M. Wallace, 2001:
Regional climate impacts of the northern hemisphere annular mode.
Science, 293, 85-89.
-
Trenberth, K. E., and D. J. Shea., 1987:
On the evolution of the Southern Oscillation.
Mon. Wea. Rev., 115, 3078-3096.
-
http://www.meteomediterraneo.com/Rubriche.asp?IDRubrica=6
-
Wallace J. M, 2000:
North atlantic oscillation/annular mode: Two paradigms--one phenomenon.
Quart. J. R. Met. Soc., 126, 791-805.
-
Wallace, J. M., and D. S. Gutzler, 1981:
Teleconnections in the geopotential heightfield during the
northern hemisphere winter. Mon. Wea. Rev., 109,
784-812.
-
Wallace J. M., and D. W. J. Thompson, 2002:
The pacific center of action of the northern hemisphere annular mode:
Realor artifact?
J. Climate, 15, 1987-1991.
- Watanabe, 2003:
Thompson D. W. J., and J. M. Wallace., 2001:
Regional climate impacts of the northern hemisphere annular mode.
Science, 293, 85-89.
-
Watanabe M., and M. Kimoto, 1999:
Tropical-extratropical connection in the atlantic atmosphere-ocean
variability.
Geophys. Res. Lett., 26, 2247-2250.
-
Watanabe M., and M. Kimoto, 2000:
Atmosphere-ocean thermal coupling in the north atlantic: A positive
feedback.
Quart. J. R. Met. Soc., 126, 3343-2369.
- Watanabe M., and M. Kimoto, 2000:
On the persistence of decadal sst anomalies in the north atlantic.
J. Climate, 13, 3017-3028.
-
Watanabe M., and M. Kimoto, 2001:
Corrigendum.
Quart. J. R. Met. Soc., 127, 733-734.
-
Yamazaki K., and Y. Shinya, 1999:
Analysis of the arctic oscillations simulated by agcm.
J. Meteor. Soc. Japan, 77, 1287-1298.
-
Zhang, Y., and I. M. Held, 1999:
A linear stochastic model of a GCM's midlatitude storm
tracks.
J. Atmos. Sci., 56, 3416-3435.
ODAKA Masatsugu, SASAKI Youhei, & TSUKAHARA Daisuke
2003-03-17
|