熱帯大気循環と対流活動の相互作用に関する 2, 3 の話題

タイトルぺージ

湿潤線形傾圧モデルの開発と応用 動機: 単純な熱源応答問題でよいか? 熱源応答の結果生じた循環によって, 積雲対流活動が変化し, さらに循環が変化するかもしれない CISK モデルの延長上の枠組でもう一度考える 3 次元湿潤線形傾圧モデル

wave-CISK

湿潤線形モデル (LBM) : 概要 先に大気場 X を求めてから, それにともなう加熱分布 FiX を求める

湿潤線形モデル (LBM) : 分解能, 物理過程等

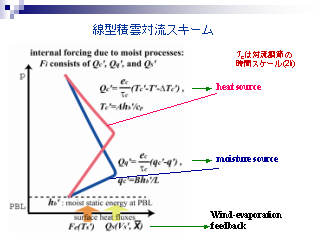
線形積雲対流スキーム: 詳細は Betts-Miller (1986), Neelin and Yu (1994) を参照 温度場, 水蒸気場の参照分布からのずれに比例して加熱が起こる 参照分布からのずれはある緩和時間で参照分布に戻るとする 緩和時間は 1 つの積雲が生成消滅する時間 (ここでは 2 時間) 0 にすると真鍋の対流調節に近付く(はず) 水蒸気の参照分布からのずれは境界層へ供給される湿潤静的エネルギー (cpT + Lq + gz) に比例する SST 依存部分と非依存部分(風速, 大気温度等に依存する部分)に分ける 負の熱源を許容する: もともと存在していた積雲が抑制されると考える A, B は計算結果が気候値を再現するように決める wave-CISK モデルの加熱と対応づけられるか ? wave-CISK モデルの加熱は下層の収束に強い依存性がある この線形積雲対流スキームでは陽に依存しない

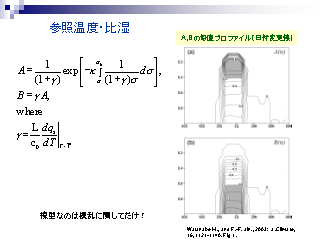
参照温度と比湿 A, B の決め方 境界層で供給された湿潤静的エネルギー h' が積雲内で保存する, という関係から得られる (らしい). 積雲内はほとんど飽和していると考える

湿潤モデルの Gill 応答 (1) 基本場は静止大気, SST は東西非一様 湿潤モデルには下降流にともなう冷却偏差が現れる それによって応答範囲が狭くなる ケルビン波の位相速度がどうなっているか確認する必要がある モデル設定の違い 乾燥モデルでは SST 依存部分がない 乾燥モデルには湿潤モデルで得られた加熱偏差のみ与える

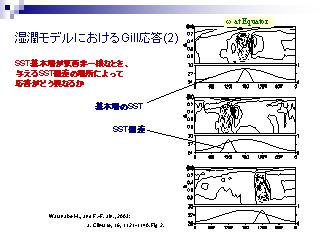
湿潤モデルの Gill 応答 (2) 基本場の SST は東西非一様 SST 偏差上の上昇流の大きさはあまり変わらない SST 偏差の東側にある下降流の大きさは変わる 基本場の SST が高い程, 積雲対流の抑制効果が大きいため

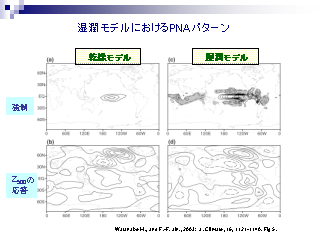
湿潤モデルにおける PNA パターン

湿潤線形モデルの応用 1 熱帯の熱強制に対する大気の応答

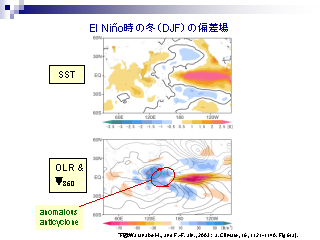
エルニーニョ時の冬 (DJF) の偏差場 (上) SST (下) OLR と 850 hPa 面流線関数 SST 正偏差は東太平洋に集中 OLR 偏差は太平洋全体に広がる 西太平洋の高気圧偏差は東アジア域に温暖湿潤な空気を輸送

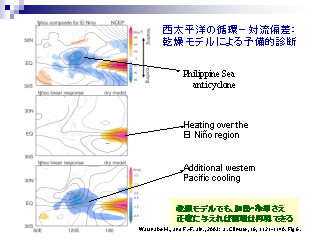
西太平洋の高気圧偏差: 乾燥線形モデルによる実験 基本場は気候値 (上) NCEP 観測値 (中) 東太平洋に加熱 (下) 東太平洋に加熱 + 西太平洋に冷却 加熱と冷却をきちんといれると乾燥モデルでも西太平洋の高気圧偏差が再現できる

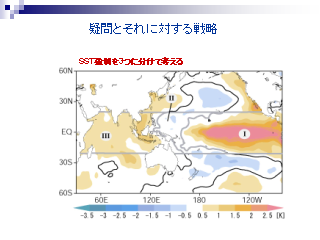
疑問とそれに対する戦略 熱帯の SST 偏差にともなう強制に注目 3 つの領域に分割, それぞれの偏差にともなう強制を線形モデルに与えて 応答を調べる モデルが線形なので結果を解釈しやすい

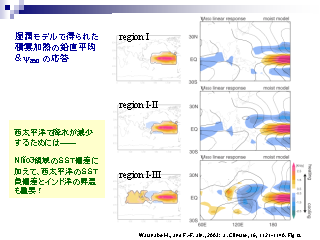
線形モデルの結果: 鉛直平均した加熱・冷却の偏差と 850 hPa 面流線関数 基本場は気候値 領域 I 〜 III へと順番に強制を加えていく I だけ: 西太平洋の高気圧偏差はない I + II: 西太平洋の高気圧偏差は少し現れる I + II + III: 西太平洋の高気圧偏差は強まる 西太平洋の高気圧偏差には西太平洋の SST 低下とインド洋の SST 上昇が寄与

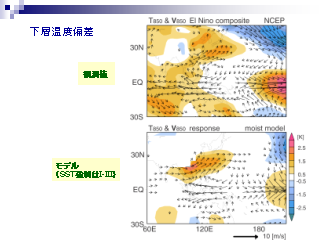
大気下層の温度偏差: 850 hPa 面の気温偏差 (上) NCEP 観測 (下) 線形モデル モデルでは I + II + III の強制, 観測される高気圧偏差循環を再現

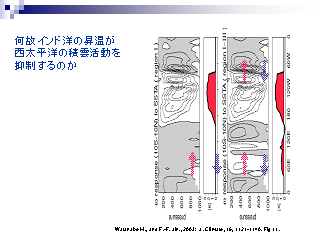
インド洋 SST 偏差による西太平洋の積雲活動の抑制メカニズム 赤道 (10S-10N) における鉛直流の経度鉛直断面 (上) 領域 I の強制のみ (下) 領域 I - III の加熱 (図なし) 領域 I にだけ強制を与えると, SST 正偏差領域で上昇流, 東側で下降流. 西側も弱い下降流 領域 I-III に強制を加えると, 領域 III の強制にともなう下降流が 西太平洋に現れる.

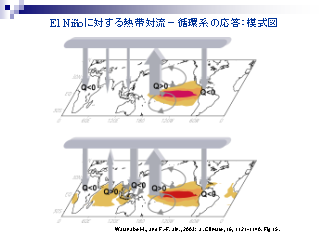
エルニーニョに対する熱帯対流-循環系の応答: 模式図 インド洋の SST 偏差によって西太平洋の下降流が強まる

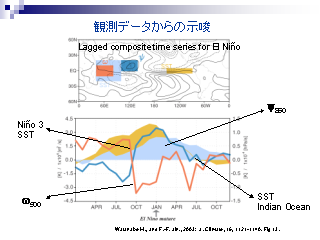
観測データからの示唆 インド洋 (領域III)の SST の上昇は Nino3 (領域I) にくらべ遅れる インド洋の鉛直流: ある時点で下降流ら上昇流に突然変化する 西太平洋の高気圧偏差: インド洋の鉛直流が上昇流になるのとほぼ同時に発生する

まとめ 1

湿潤線形モデルの応用その 2 固有値問題

Madden-Julian 振動: 過去の研究

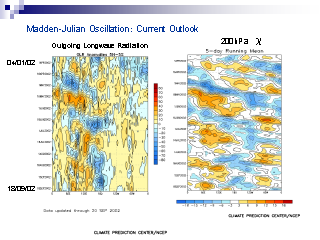
最近の Madden-Julian 振動 2002/01/04-2002/09/18 の (左) OLR と (右) 200 hPa 面の速度ポテンシャル

wave-CISK の問題点と提言

Madden-Julian 振動を調べるための湿潤線形モデル 鉛直に 11 層, 東西波数は 6 現実的な消散項を考慮すると系は安定であることに注意 wavw-CISK では不安定モードが出やすいことと異なる

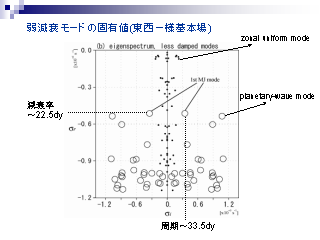
弱減衰モードの固有値 (東西一様基本場) 黒丸: 東西一様なモード どのような空間構造を持つのか? 白丸: 東西に波状構造を持つモード 東西一様なモードの方が減衰率が小さい 一番減衰しない波状構造を持つモードを知りたい 進行波か定在波かはわからない

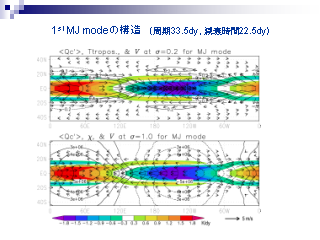
1st. MJ モードの水平構造 速度場と鉛直平均加熱率 (上) 上層, 等値線は温度 (下) 下層, 等値線は速度ポテンシャル

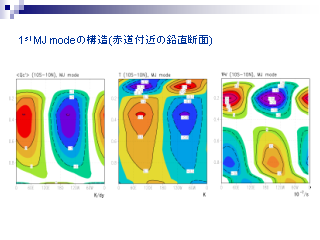
1st. MJ モードの鉛直断面 赤道 (10S-10N) 東西鉛直断面: (左) 加熱率 (中) 温度 (右)水平収束 下層では摩擦のため加熱域の東側に水平収束が生じる 10S-10N の平均であることに注意. 赤道直上では加熱域の真下で収束 Matsuno (1966) を参照. 赤道上の地衡風運動を考えると, 加熱の東側では赤道上に収束, 西側では発散となる 水平収束により次の対流が加熱域の東側に発生する wind-evaporation feed back が働いている可能性あり 地表付近に存在する薄い加熱, 冷却領域がそれ

次のステップ 基本場に熱帯東西循環を加える

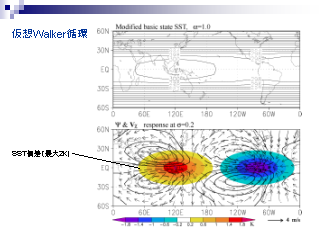
仮想 Walker 循環 基本場に東西 SST 偏差を加える (上) 生の SST (下) SST 偏差と線形モデルで求められた定常応答としての上層の流線関数と発散風

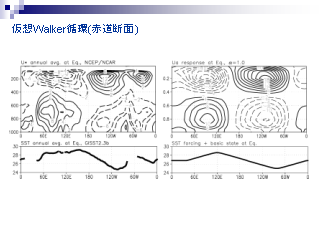
仮想 Walker 循環: 観測との比較 赤道上東西風の東西鉛直断面 (左) NCEP/NCAR (右) 線形モデルの応答

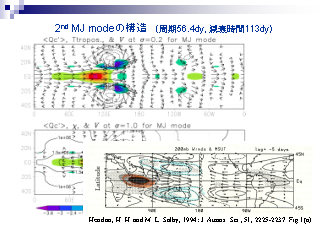
2nd. MJ モードの水平構造 上記の東西非一様成分を加えた基本場に対する固有地問題を解く. 最も減衰率の小さいモードを 2nd MJ モードとする 速度場と鉛直平均加熱率 (上) 上層, 等値線は温度 (下) 下層, 等値線は速度ポテンシャル ある位相における分布, 位相か変わると異なるパターンが現れる さまざまな東西波数の構造の重ね合わせのような構造 加熱, 冷却領域が局在している 赤道上はほとんど西風 観測と比べるとインド洋で対流活動が活発な時期のパターン (Hendon and Salby, 1994) に比較的似ている

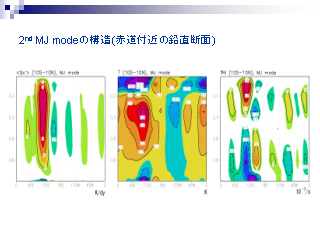
2nd. MJ モードの鉛直断面 赤道上 (10S-10N) の東西鉛直断面: (左) 加熱率 (中) 温度 (右)水平収束

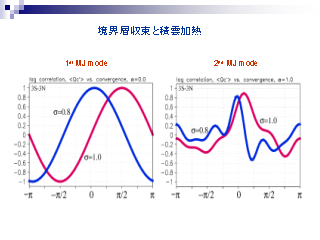
境界層収束と積雲加熱

なぜ 2nd MJ モードは東半球に偏在するのか?

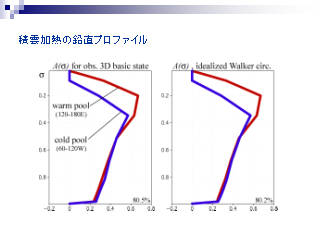
積雲加熱の鉛直プロファイル

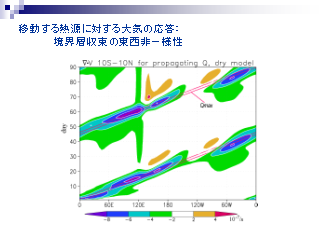
移動する熱源に対する大気の応答

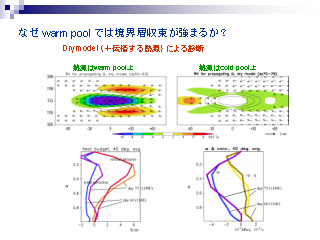
なぜ warm pool では境界層収束が強まるのか?

MJ モードの基本場東西非一様性への依存性 東西非一様性を変えながら固有値問題を解く 東西一様基本場の MJ モードと非一様基本場 ML モードとの連続的に理解することを目指す

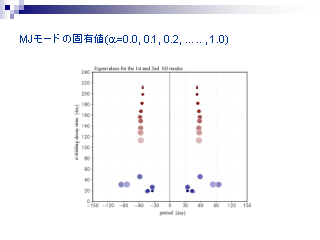
MJ モードの固有値 東西非一様性を弱くしていくと, 2nd MJ モードは水平一様基本場の東西一様モードに重なる

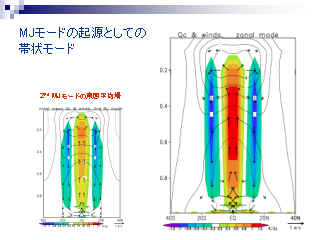
MJ モードの起源としての帯状モード 加熱率の緯度高度分布と子午面循環 (左) 2nd ML モードの東西平均場 (右) 東西一様基本場の東西一様モード 2nd ML モードと東西一様基本場の東西一様モードの構造はよく似ている 東西一様基本場の東西一様モード: 東西風は下層で東風, 上層で西風 ハドレー循環はそもそも CISK になりうる

MJO の起源は? Hayashi and Sumi (1986) では東西一様成分の寄与を指摘しているが…

まとめ 2

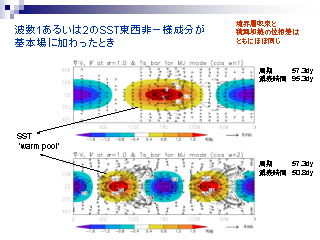
波数 1 あるいは 2 の SST 東西非一様成分が基本場に加わったとき

CISK: 第二種の条件付き不安定

AGCM 実験の動機 線形モデルの東西一様モードに対応するパターンを得られるか?

水惑星実験設定 MCA-run: 標準実験, 基本場 SST 東西一様 MCAWV-run: 基本場 SST 東西非一様

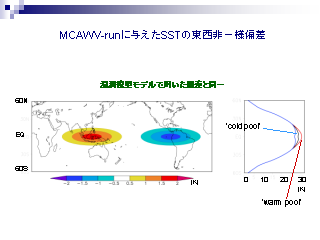
MCAWV-run に与えた SST の東西非一様偏差

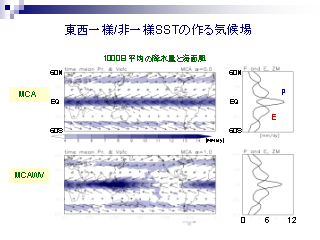
東西一様/非一様 SST の作る気候場 1000 日平均の降水量と海上風

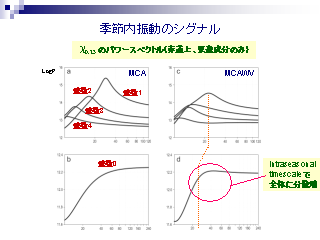
季節内振動のシグナル 上層の速度ポテンシャルのパワースペクトル 東西非一様な場合, 波数 0 成分の パワー MAX となる振動数は波数 1 成分のパワーが MAX となる振動数よりも高周波側にある.

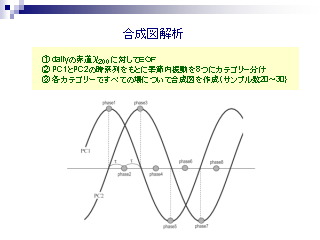
合成図解析

合成図: MCA-run (1) phase 3 の偏差パターン (左上) 上層の発散風と速度ポテンシャル (右上) 海上風 (左下) 圏界面の温度 (右下) 蒸発量

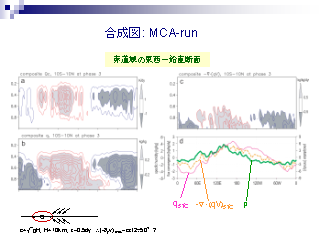
合成図: MCA-run (2) pahse 3 の経度高度断面 (左上) 凝結加熱 (右上) 水蒸気収束 (左下) 水蒸気混合比 (右下) 地表の気圧, 水蒸気混合比と収束

合成図: MCAWV-run (1) phase 1 の偏差パターン (左上) 上層の発散風と速度ポテンシャル (右上) 海上風 (左下) 圏界面の温度 (右下) 蒸発量

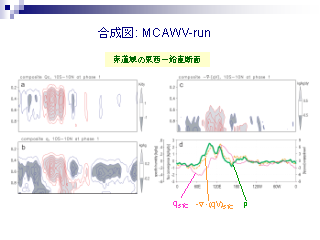
合成図: MCAWV-run (2) pahse 1 の経度高度断面 (左上) 凝結加熱 (右上) 水蒸気収束 (左下) 水蒸気混合比 (右下) 地表の気圧, 水蒸気混合比と収束

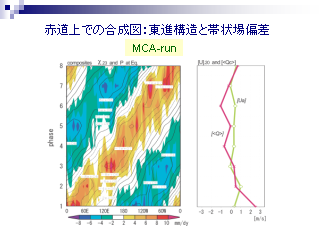
赤道上での合成図: 東進構造と帯状場偏差 (MCA-run) 赤道上層の速度ポテンシャルと地表気圧の時間経度断面 東進して地球を一周する

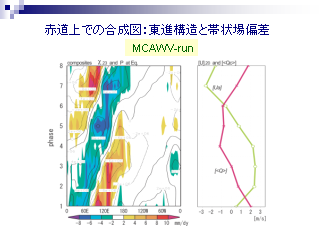
赤道上での合成図: 東進構造と帯状場偏差 (MCAWV-run) 赤道上層の速度ポテンシャルと地表気圧の時間経度断面 SST の正のアノマリをおいた領域にのみ存在する

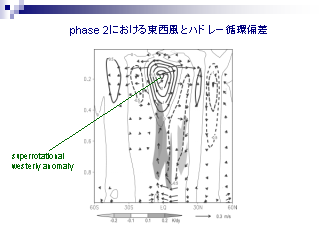
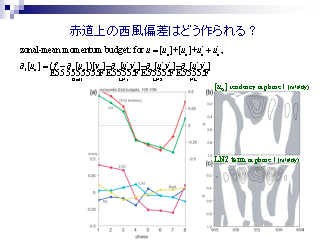
phase2 における東西風とハドレー循環偏差

赤道上の西風偏差はどう作られる? 東西風の変化の様子に一番効くのは, 気候値の波成分とそれからのずれによる運動量輸送

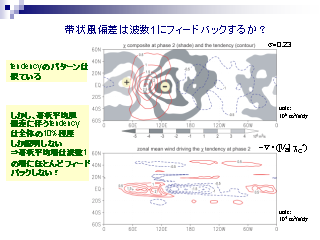
帯状風偏差は波数 1 にフィードバックするか? phase 2 における上層の速度ポテンシャルの分布と変化率 東西平均場の偏差による寄与は速度ポテンシャル変化率全体の 10 % 程度でしかない

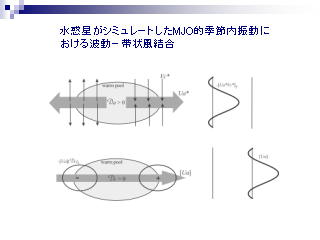
水惑星 GCM がシミュレートした MJO 的季節内振動における波動-帯状風相互作用

まとめ 水惑星実験の結果は固有値解析の仮説を支持しない

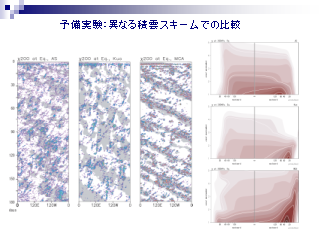
予備実験: 異なる積雲スキームでの比較 東西一様基本場を与えた場合の赤道降水量の時間経度断面図 (左) Arakawa-Shubert (中) Kuo (右) 対流調節: もっとも東進構造が顕著に現れる

参考文献

• Betts A. K., and M. J. Miller, 1986: A new convective adjustment scheme. part ii: Single column tests using gate wave, bomex, atex and arctic air-mass data sets. Quart. J. R. Met. Soc., 112, 693-709.

• Neelin D., and J.-Y. Yu., 1994: Modes of tropical variability under convective adjustment and the madden julian oscillation. part i: Analytical theory. J. Atmos. Sci., 51, 1876-1894.

  Lau et al., 1988: The Madden-Julian oscillation in an idealized general circulation model. J. Atmos. Sci., 45, 3810-3832.

• Watanabe M., and F.-F. Jin., 2003: A moist linear baroclinic model: Coupled dynamical convective response to el ni-no. J. Climate, 16, 1121-1139.

• Hendon, H. H. and M. L. Salby, 1994: The life cycle of the Madden Julian oscillation., J. Atmos. Sci., 51, 2225-2237.

• Hayashi Y-Y., and A. Sumi., 1986: The 30day oscillation simulated in an aqua planet model. J. Meteor. Soc. Japan., 64, 451-467.

• Lim, H., Lim, T.-K. and Chang, C.-P., 1990: Reexamination of wave-CISK theory: Existence and properties of nonlinear wave-CISK modes. J. Atmos. Sci., 47, 3078-3091.

• Lau K.-M., and L. Peng., 1987: Origin of low-frequency (intraseasonal) oscillations in the tropical atmosphere. part i: Basic theory. J. Atmos. Sci., 44, 950-972.

• Wang B., 1988: Dynamics of tropical low-frequency waves: An analysis of the moist kelvin wave. J. Atmos. Sci., 45, 2051-2065.

• Emanuel K. A., 1987: An air-sea interaction model of intraseasonal oscillations in the tropics. J. Atmos. Sci., 44, 2324-2340.

• Matsuno T., 1966: Quasi-Geostrophic Motions in the Equatorial Area. J. Meteor. Soc. Japan., 44, 25-43.