/地球流体セミナー
/講演資料一覧
/2004-03-23/
成層回転乱流の数値計算と大気スペクトル:
門前編
高木 征弘(東大・理)
2004 年 3 月 23 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|
|
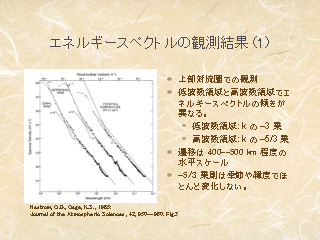
エネルギースペクトルの絵
- 上部対流圏の観測
- 航空機観測による大気スペクトル
- 400--500 km をさかいに,
- 大スケールは -3 の傾き
- 小スケール: k の -5/3 乗の傾き
今日の本題は, -3, -5/3 乗則を理論的に説明すること.
|
|
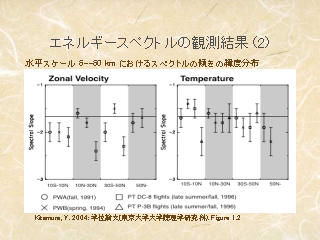
エネルギースペクトルの絵
- 対流圏全体の絵
- 季節変化はない, というのが定説
- エネルギースペクトルは緯度変化しない
- 緯度に依存しない, 値は -5/3 というのが定説
|
|
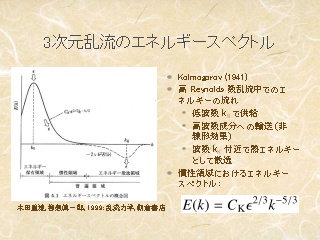
3 次元乱流のエネルギースペクトル
- Kolmogorov (1941)
- 波数の小さい領域: エネルギーが流体に入る
--> 注入されたエネルギーは波数の小さい方へ流れる
- Kolmogorov scale Kk で熱として散逸
- 観測との関係はまた後程議論.
|
|
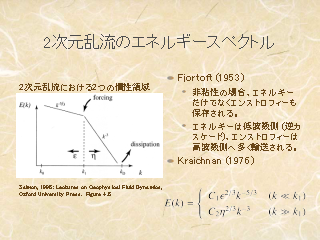
2 次元乱流のエネルギースペクトル
- エネルギーとエンストロフィーの保存に着目
- エネルギーの全部が低波数にいくわけではなく,
大部分が低波数側へ.
- 高波数へ行ったエネルギーとエンストロフィーは, 熱として散逸
- エネルギー輸送の方向が 3 次元乱流とは異なることに注意
- フォーシングは小スケールの積雲対流など
|

|
準地衝風乱流
- Charney (1971)
- ポテンシャルエンストロフィーが保存
- 2 次元乱流との類似を指摘
- 観測との対比
- 低波数側の -3 乗のスペクトルは 2 次元乱流
- 高波数側の -5/3 乗のスペクトルは 3 次元乱流?
- -3/5 乗の領域はスケールが小さすぎて QG は使えないという説あり
--> 3 次元乱流的?
|

|
成層性乱流
- 成層が十分強いと仮定し, 時間スケールとして移流と成層の 2 つを用いる
- 成層が強ければ 2 次元乱流的なエネルギーの逆カスケードとして理解できる
<--> Charney (1971)
- Lilly では「重力波は対象とする領域から素早く射出されてしまうので関係ない」
と言っているらしいが, 領域の外からやってくる成分もあるはずなので,
この考え方はおかしい(?)
|

|
Lilly (1983) のスケーリング
- 浮力振動数でスケーリングし, フルード数が十分小さい近似をすると,
内部重力波の式が得られる.
- 移流時間でスケーリングし, フルード数が十分小さくロスビー数が大きい近似をすると,
順圧渦度方程式が得られる.
- 鉛直移流のスケーリングには成層の効果を考慮しているらしい
(単純にスケーリングすると水平移流と同じ)
- f のつき方が違う.
- コリオリには 1/R
- f^2, 1/R は無視
- 2 次元的な渦度方程式が残る
|
|
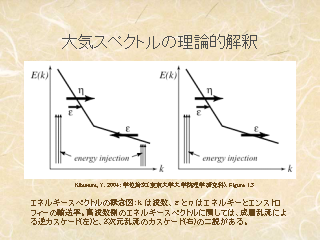
大気スペクトルの理論的解釈: いままでのまとめ
左図
- エネルギー注入は低波数, 高波数の 2 つ
- 高波数でのエネルギー注入は, 例えば積雲対流
- 低波数側では QG でエンストロフィー(エネルギー)のカスケード
- 高波数側では成層乱流による逆カスケード(Lilly)
- Lilly の理論に従えば,
積雲よりも小さなスケールでは -3 乗,
さらにスケールが小さくなって成層が効かなくなると -5/3 乗になるはず
右図
- 低波数側では QG でエンストロフィー(エネルギー)のカスケード
- 高波数では乱流が 3 次元的になり, k の -5/3 乗が説明される(Charney)
どっちの説が正しいのかはよくわからない
|

|
3 次元乱流の理論
|

|
3 次元乱流の性質
- 乱流レイノルズ数における長さと速度のスケールは,
エネルギー保有領域(もっとも大きい渦)の長さと速度のスケール
- 非線形項が卓越. スケールは一番大きい渦のもつスケール
- 渦の最大スケールに粘性は効かない, 小さなスケールでは粘性が無視できない
- 微小擾乱に対する不安定性:小さな渦が次々と生成されることを意味しているようだ
|

|
基礎方程式
|

|
粘性作用の性質
- 粘性項の形式から, Re が大きく, νが小さいなら, k^2 で効く
|

|
速度相関テンソルとエネルギースペクトル
- 波数空間の積分として表現
- エネルギースペクトルの定義が得られる
|

|
エネルギースペクトルのフーリエ表現
- エネルギースペクトルは速度のフーリエ成分のアンサンブル平均として表現
|

|
エネルギースペクトル方程式
- k + p + q = 0 となるフーリエ成分間でエネルギーが保存
- 非線形項がエネルギーのやりとりを
|
|
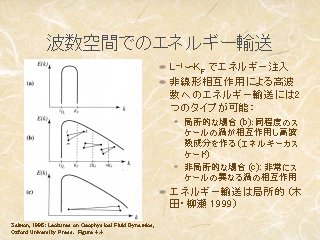
波数空間でのエネルギー輸送
- 初期条件としてあるエネルギーを与える(上図)
- 非線形項による相互作用
- 局所的な輸送: 近い波数同士が相互作用(中図)
- 非局所的な輸送: 波数の大きく異なる成分同士が相互作用(下図)
- 数値実験などによれば, エネルギー輸送は局所的
|
|
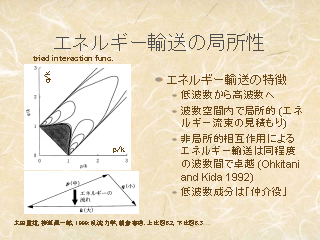
エネルギー輸送の局所性
- 理論的にも数値計算でも同様の絵が書ける
- 低波数成分は仲介役, 物理的には大きな渦に小さな渦が乗っかっていて,
大きな渦は少し変形しながら移流されているだけ, という状況を想定すればよい
|

|
小規模運動の普遍性
- 十分に高波数へカスケードした後はどうなるか, という問題
- 小規模運動になってしまったら, 大スケールの時の情報は失われているだろう
- 小規模運動は統計的に等方的かつ普遍的になると期待される
--> Kolmogorov の仮定
|

|
Kolmogorov の理論
- 仮説が 2 つ
- 確率分布関数は速度の相関テンソルみたいなもの
- 慣性領域では粘性に依存してはいけない
|

|
第 1 仮説からの帰結
- Kolmogorov 長さのスケールではレイノルズ数は 1 程度, 粘性が効く
|

|
第 2 仮説からの帰結
- スケール大きくて粘性が働かない --> 普遍関数として波数の gamma 乗
- 粘性に依存しないようにするには, gamma = - 5/3
- 慣性領域での渦の特性時間と特性速度を与えた
- 1 回のカスケードにかかる時間が小さくなっていく
- 普遍関数の置き方に正当性は, 粘性とキャンセルアウトできるか否かだけ
|
|
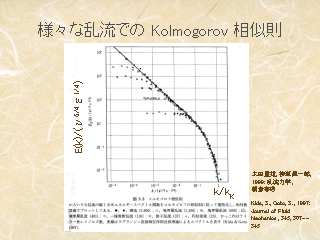
様々な乱流での Kolmogorov の相似則
- 普遍関数と実験の整合性のチェック
- ずれはあるものの, 波数が小さいと -5/3 乗則.
- k/kk=10 程度以下になると -5/3 の線からずれる
|
|
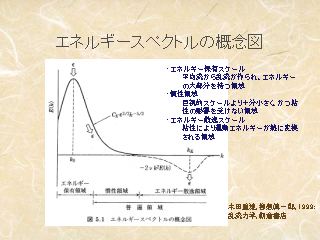
エネルギースペクトルの概念図
- 慣性領域では k -5/3 乗則
- エネルギー散逸領域では熱に散逸
|

|
kolmogorov 理論の仮説
- 非粘性の極限でエネルギー散逸率が有限の値に漸近する
- エネルギー伝達率がカスケードの各ステップで一定
Euler 方程式が有限時間で発散する
- εの時空間変動が大きい
-->
|

|
2 次元乱流の理論
- エネルギーとエンストロフィーの保存
- 3 次元乱流ではエネルギー保存だけ考慮
- 順圧非発散渦度方程式で考える
|

|
エネルギーとエンストロフィーのカスケード
- Salomon の教科書での説明
- エネルギーは低波数に多く輸送される
- エンストロフィーは高波数側へ多く輸送される
- 三角形が作れるように波数を選択する (k, 2k, k/2 ではダメ)
- この OHP の k0, k1, k2 では三角形が作れない.... でも定性的にはこんなもの
|
|
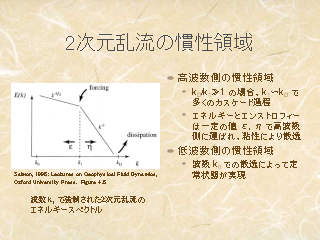
2 次元乱流の慣性領域
- 高波数側: forcing と粘性散逸の間で慣性領域が形成
- 低波数側: 領域の最大サイズでエネルギーが溜るはず.
何らかの散逸が生じて定常状態へ.
- 次元解析で巾乗則を求める際には, εとエータのどちらかを無視
- 低波数側ではエネルギー散逸率を一定と考える
- 高波数側ではエンストロフィー散逸率を一定と考える
|

|
高波数の慣性領域
- 非粘性極限でエンストロフィー供給率(=散逸率)が有限であるとする
|

|
低波数側の慣性領域
- 高波数側と同様の考察により, E(k) は k とエータに依存
- 3 次元乱流とエネルギーの運ばれる向きが逆: 逆カスケード
|

|
2 次元乱流と地球大気との関係
- 地球大気はだいたい 2 次元的(QG 乱流)
- Kd よりも大きくなった場合には, 考え方は 2 通り
- 乱流が 3 次元的に
- 成層の効果で 2 次元的なまま.
|

|
まとめ
- 400-500 km 以下のスペクトルの解釈はいろいろあるらしい
- 2 次元乱流でも -5/3 でダウンワードカスケード?
- 非等方なので 3 次元乱流にはならないだろう
- 3000 km 以上のスペクトルは山岳がなくとも不明瞭では? (林)
- 打ち止めだから(対数軸ではそれ以上のスケールはあまりよく見えないだろう)
|

|
Kolmogorov's turbulence definition
|

|
カスケードの写真
|
|
|
参考文献
- Charney, J.G., 1971:
Geostrophic turbulence, J. Atmos. Sci., 28, 1087--1095.
- Fjortoft, R., 1953:
On the changes in spectral distribution of kinetic energy for
two dimensional, nondivergent flow, Tellus, 5, 225--230.
- Kitamura, Y. 2004:
Numerical study on energy cascades in stratified turbulence with the application to the atmospheres, 学位論文(東京大学大学院理学研究科)
- Kitamura, Y. and Y. Matsuda, 2004:
Numerical Experiments of Two-Level Decaying Turbulence on a Rotating Sphere,
Fluid Dyn. Res., 34, 33--57.
- Kida, S., Goto, S., 1997:
A Lagrangian direct-interaction approximation for homogeneous isotropic turbulence,
Journal of Fluid Mechanics, 345, 307--345
- 木田重雄, 柳瀬眞一郎, 1999: 乱流力学, 朝倉書店
- Kolmogorov, A.D., 1941:
The local structure of turbulence in incompressible viscous fluid for
very large Reynolds numbers, and Dissipation of energy in the locally
isotropic turbulence.
English translations: Proc. Roy. Soc. Lon. A434,
Turbulence and stochastic prosesses: Kolmogorov's ideas 50 years on 9--17.
- Klomogorov, A.D. 1962:
A refinement of previous hypotheses concerning the local structure of
turbulence in a viscous incompressible fluid at high Reynolds number,
J. Fluid Mech., 13, 82--85.
- Kraichnan, R.H., 1967:
Inertial ranges in two-dimensional turbulence,
Phys. Fluids., 10, 1417--1423.
- Landau, L.D. and Lifshitz, E.M., 1954:
Mekhanika sploshnykh sred(Continuum Mechanics),
Moscow: Gos. Izd. Tekh. Teor. Lit.
- Lilly, D.K., 1983:
Stratified turbulence and the mesoscale variability of the atmosphere,
Journal of the Atmospheric Sciences, 40, 749--761
- Nastrom, G.D., Gage, K.S., 1985:
A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft,
Journal of the Atmospheric Sciences, 42, 950--960
- Ohkitani, K., Kida, S., 1992:
Triad interactions in a forced turbulence,
Physics of Fluids, 4, 794--802
- Riley J.J., Metclfe, R.W., Weissman, M.A., 1981:
Direct numerical simulations of homogeneous turbulence in density stratified fluids,
in Non linear properties of internal waves, La Jolla Institute,
AIP Conference Proceedings 76, 79--112.
- Salmon, 1998: Lectures on Geophysical Fluid Dynamics,
Oxford University Press.
- Angrei Nikolaevich Kolmogorov,
http://www.kolmogorov.com/
|
SUGIYAMA Ko-ichiro & ODAKA Masatsugu
2004-04-27
|

































