/地球流体セミナー
/講演資料一覧
/2004-03-23/
成層回転乱流の数値計算と大気スペクトル:
地球シミュレータでのパワースペクトルの結果
高橋 芳幸(神戸大・理)
2004 年 3 月 23 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|
|
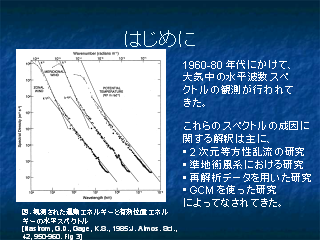
はじめに
|
|
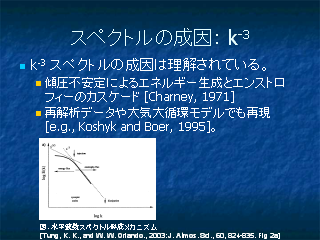
スペクトルの成因: k^-3
|
|
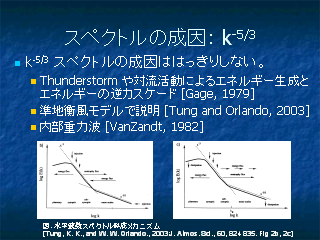
スペクトルの成因: k^-5/3
- Tung and Orland, 2003 は中緯度のチャネルモデル
- 総観規模擾乱による強制から, 高波数側へエネルギー, エンストロフィーが輸送
- 重力波のスペクトルが -5/3
|

|
過去の計算では
- 解像度が足りなかった
- Hamilton の GFDL SKYHI モデルでは再現できているけど, 他モデルではどうなっているか把握する
|

|
本研究の目的
|

|
AFES
- 水平拡散は k^-5/3 が再現できるようにチューン
|
|
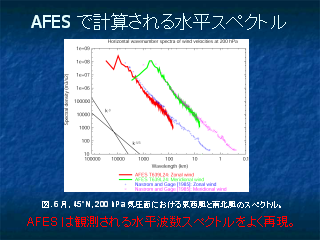
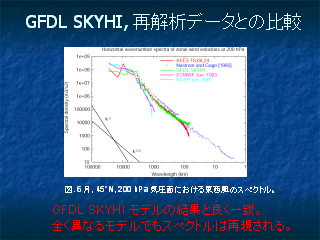
AFES で計算された水平スペクトル
- 図の縦横比の関係で, k^-3 と k^-5/3 の傾きが同じように見えてしまうことに注意.
-
|
|
モデルの結果の比較
|

|
パラメタ, パラメタリゼーション依存性
- 水平拡散係数, 積雲対流パラメタリゼーション依存性を調べる
|

|
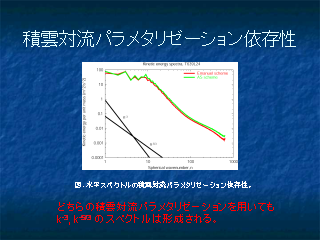
水平拡散係数依存性
|
|
積雲パラメタリゼーション
- おおざっぱにはスペクトルの特徴は変わらない
- 全エネルギーという見地からは, Arakawa Schubert(AS) の方が優位に大きい
- 高解像度では AS は効かないという説もあるけど....
細かなパラメタ, パラメタリゼーションを変えても問題なさそう
|

|
降水分布の依存性
|
|
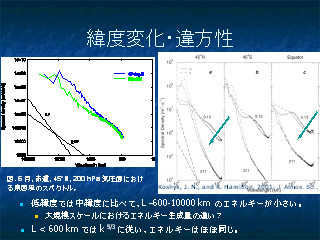
経度変化, 異方性
- 赤道の方がエネルギー源が少ないことと整合的
- 右図は Hamilton の GFDL の結果
- GFDL のモデルでは赤道域でエネルギーが大きい
|

|
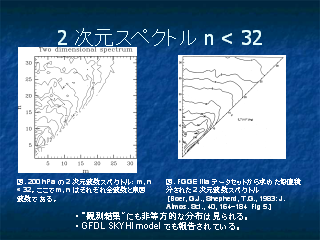
2 次元スペクトル n < 32
- 波数 32 までプロット
- 非等方的な結果は観測でも報告されている(FGGE-IIIa; Boer and Shepherd)
|
|
2 次元スペクトル n < 32
- 非等方的な結果は観測でも報告されている(FGGE-IIIa; Boer and Shepherd)
|

|
2 次元スペクトル
|

|
Nozawa and Yoden (1997)
|

|
高度依存性
- 過去の研究から 200 hPa での値が最も大きい
-
|
|
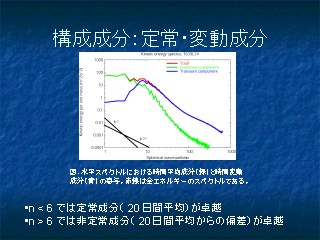
構成成分
|

|
回転, 発散
- 全ての波数で回転成分が卓越
- 発散することは無視することはできない
-
|

|
運動エネルギー収支
- k の -5/3 乗則に対して何かしらの見解を得たい
-
-
|

|
運動エネルギー
|
|
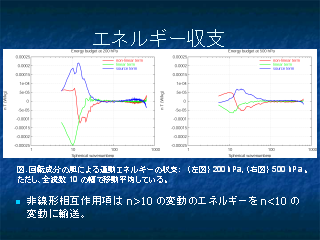
エネルギー収支
- ここでは鉛直方向で分割
- 他の研究(Kitamura, 2004)では鉛直方向に積分している
|
|
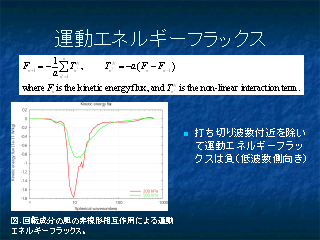
運動エネルギーフラックス
- 全ての波数領域でフラックスが負 = upward cascade
-
-
|

|
k^-5/3 の成因
- フラックスは低波数を向いている
- 彼らは全波数についての計算なので厳密には違う
- 回転成分だけでフラックスを計算している.
|

|
k -5/3 の成因
- 定量的な値を決める上では積雲対流パラメタリゼーションは重要
|

|
大規模場への影響
|
|
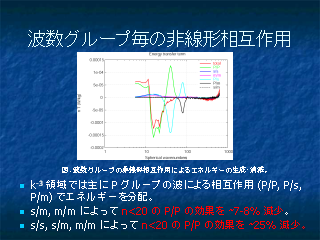
波数グループ毎の非線形相互作用
- triad interaction の考えを利用
- 小さい波数との相互作用もけっこう効くようだ
-
|

|
水平解像度依存性
|

|
まとめ
- QG の世界で折れ曲がる. この世界でも同じというには, エネルギーの流れがどうなっているのか知る必要がある.
|
|
|
参考文献
- Boer, G.J., Shepherd, T.G., 1983:
Large-scale two-dimensional turbulence in the atmosphere.
Journal of the Atmospheric Sciences, 40, 164--184
- Charney, J.G., 1971:
Geostrophic turbulence, J. Atmos. Sci., 28, 1087--1095.
- Emanuel, K.A., Zivkovic-Rothman, M., 1999:
Development and evaluation of a convection scheme for use in climate models.
Journal of the Atmospheric Sciences, 56, 1766--1782
- Gage, K.S., 1979:
Evidence for a k/sup -5/3/ law inertial range in mesoscale two-dimensional turbulence.
Journal of the Atmospheric Sciences, 36, 1950--1954
- Koshyk, J. N., and G. J. Boer, 1995:
Parameterization of Dynamical Subgrid-Scale Processes in a Spectral GCM,
JAS, 52, 965--976
- Koshyk, J. N., K. Hamilton, and J. D. Mahlman, 1999:
Simulation of the k^5/3 Mesoscale spectral regime in the GFDL SKYHI
General Circulation Model, GRL, 26, 843--846
- Koshyk, J. N., and K. Hamilton, 2001:
The Horizontal Kinetic Energy Spectrum and Spectral Budget Simulated by
a High-Resolution Troposphere-Stratosphere-Mesosphere GCM,
JAS, 58, 329--348
- Nastrom, G.D., Gage, K.S., 1985:
A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft,
Journal of the Atmospheric Sciences, 42, 950--960
- Nozawa, T. and Yoden, S. 1997:
Spectral anisotropy in forced two-dimensional turbulence on a rotating sphere.
Physics of Fluids, 9, 3834---3842
- Straus, D.M., Ditlevsen, P., 1999:
Two-dimensional turbulence properties of the ECMWF reanalyses
Tellus, Series A, 51A, 749--772
- Tung, K. K., and W. W. Orlando, 2003:
The k^-3 and k^-5/3 Energy Spectrum of Atmospheric Turbulence:
Quasigeostrophic Two-Level Model Simulation,
JAS, 60, 824--835
- VanZandt, T.E., 1982:
A universal spectrum of buoyancy waves in the atmosphere.
Geophysical Research Letters, 9, 575--578
|
SUGIYAMA Ko-ichiro
2004-03-23
|






























