/地球流体セミナー /講演資料一覧 /2004-09-13/

A Tutorial on the Stratospheric Dynamics

 余田 成男(京大・理)
2004 年 9 月 14 日
講演ビデオを見るには, 以下の各スライド画像をクリックし, 左上に表示される「ビデオ開始」をクリックしてください.
講演資料: [pdf], [ps]
タイトルぺージ

教科書, など

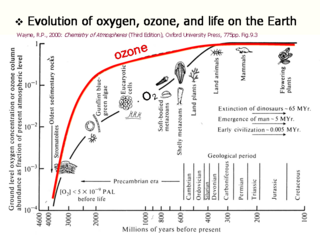
大気の進化
  • N2 はおそらく有機物からの寄与が大きかったと考えられる
  • C, N はおそらく CO, NH3 のような形で最初脱ガスしたと考えられる
  • 水に溶けた CO2 は水中の岩石に固着(炭酸塩)する. その結果 CO2 は海洋に溶け続ける. CO2 の溶解度はそこそこなので, CO2 濃度が上がり過ぎると溶けられなくなる.

酸素,オゾンの進化と地球上の生命
  • 大気中のオゾン量の増加

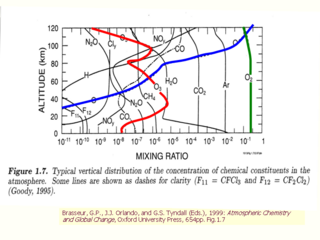
標準的な大気中の化学成分濃度の鉛直分布
  • Ar, O2 のように寿命の長い化学種は混合比一定 --> よく混合している
  • 80 km くらいまでを指して turbosphre という
  • 絵は global mean なのか? 昔は中緯度の平均を引くことが多かったが.... 参考文献を見ないと良くわからない
  • Ar の混合比が少なくなるのは, 光解離するからではなく, 重力分離するため.

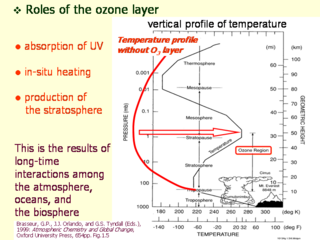
オゾン層の役割
  • オゾンによる紫外線吸収によって鉛直温度が決まる
  • オゾンがなければ成層圏がなかっただろう

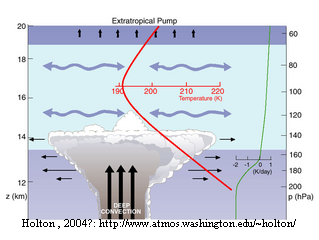
対流圏,成層圏の遷移領域
  • ここが圏界面というようにきっぱりと切れるものではない
  • 絵では温度と物質では対流圏界面の高度が異なる
  • 「遷移領域」という言い方を使う
    　　--> 強い積乱雲が成層圏まで貫入するというイメージは崩壊した
  • 「遷移領域」の「ニョロニョロ」は何を意味しているのか?
    --> 速い水平輸送を意味する

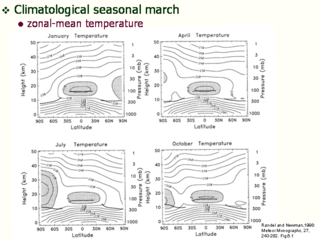
気候学的季節変動 (子午面平均温度場)
  • 子午面断面図
  • ハッチの領域は 210 Kよりも温度の低い領域
  • 白夜の極が高温となる
  • 北極の冬と南極の冬では 20 km 高度の温度が約 20 K 異なる
    --> 放射では説明できない. 力学的な影響
  • 赤道の温度は 1 年周期. 太陽が 2 回頭の上を通過するのに
    --> 放射では説明できない. 力学的な影響
北半球は陸が多く, 南半球は海洋 ロスビー波の励起元 本日は最終的には上記の原因を語る

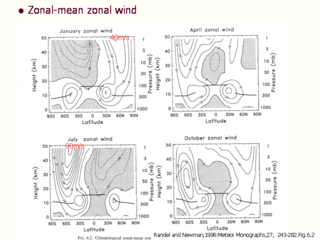
気候学的季節変動 (子午面平均東西風)
  • polar night jet (90 m/s). オゾンホールの原因
  • 対流圏界面がつながっていない理由はよくわからない. 定義の問題?

極渦とプラネタリー波: ロスビー波の復習
  • ロスビー波を復習する

ロスビー波とは
  • ポテンシャル渦度の保存則によって支配される波
  • 流れマルチメディアを見るのが簡単. 回転が波の運動を拘束
    http://www.nagare.or.jp/mm/99/ishioka/

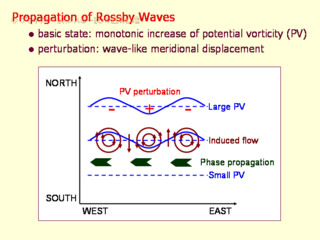
ロスビー波の伝搬
  • 基本場: ポテンシャル渦度が単調増加
  • 擾乱: 南北方向の波型の擾乱
  • 擾乱は西進する
  • 成層圏の描像は。。。。

極渦とプラネタリー波: プラネタリー波の復習
  • 波数　1, 2 の波を超長波と呼んでいた(現在は使わない)
  • Charney and Drazin (1961): 成層圏的な見方

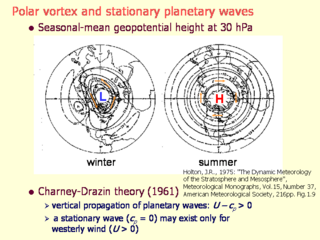
ジオポテンシャルハイトの季節平均
  • 波形で鉛直方向に伝わりうるのは, U-Cp > 0

極渦とプラネタリー波: 波と平均流の相互作用
  • 60s-70s: 波と平均流の相互作用
  • ほとんどが線形, 弱非線型解析
  • 渦 --> 波数　1, 2 の波 --> 渦
  • 80s: 砕波は波数　1, 2, 3 では記述できない.
  • McIntyre が 70 年代後半には「波」, 80 年代に「渦」と言い出す. 混乱が生じたこともあった.

より非線形な状況: 砕波するプラネタリー波
  • 成層圏でも砕波が発見. 人工衛星の分解能が向上

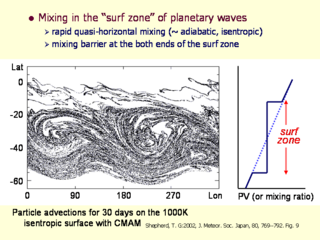
サーフゾーンにおけるプラネタリー波の混合
  • ラグランジュ粒子をまいて計算. 30 日後のスナップ
  • 良く混ざると　PV は一様化. 混合域の端は　PV の勾配がきつくなり粒子が混ざれなくなる.

中緯度ベータ面準地衡流方程式系 (1)
  • これからの話は参考資料を参照
  • 平均場は地衝流平衡, 静水圧平衡
  • 座標は対数圧力座標を用いる

中緯度ベータ面準地衡流方程式系 (2)
  • 擾乱は小さいものとして式を作る
  • 時間微分は地衝流で
  • この段階で QG 世界は閉じる --> これを基に平均場と擾乱に分ける
  • 変形することでポテンシャル渦度の式(QG-PV)

中緯度ベータ面準地衡流方程式系 (3)
  • QG-PV の式を書き直したもの
  • 1960s の天気予報モデルの基礎
    • 変数の数が少ない. 重力波なし

オイラー平均方程式系 (1)
  • 平均の作り方: 360 度平均
  • 地衝流: 平均されたもの

オイラー平均方程式系 (2)
  • フラックスの収束で運動が励起
  • 温度と風は独立に変化できない.
  • 60s--70s はこのシステムでものを見ることが主流であった
  • オイラー平均で行うと, 冬の成層圏で大きな逆循環が生じる. 直観的と反する
  • u_a は y-運動方程式から解析的に求める

オイラー平均方程式系 (3)
  • 波成分で見た場合
  • 波を記述
  • 右辺に 2 次の項をまとめてある
  • 式を閉じるためには 2 次の擾乱項を決める機構が必要 --> Closure
    • 2 次の項は 0 --> 線形化

オイラー平均方程式系 (4)
  • dq/dy を実効的ベータと呼ぶ
  • PV の勾配があることがロスビー波の成因
  • βが滑らかでも右辺第 2, 3 項によって

変形オイラー平均方程式系 (1)
  • 速度の定義を変更して方程式系を書き換える
  • おつりが見掛け上なくなる
    • 連続の式 = 0 の形式を取れる
    • 運動方程式で波を生成する項が divF で書き表せる
  • Charney-Drazin の非加速定理(波があるだけでは加速しない)は便利. それを最大限活用したい. 見通しの良い式を作る. curl を付け足しても良い
  • ラグランジュ的見方(GLM)とも対応関係にある. ある条件(v^† w^† が等しい)だとラグランジュ的速度とみなせる.
    --> TEM がラグランジュ的見方に使われる理由

変形オイラー平均方程式系 (2)
  • E-P フラックス
  • さらに変形することで残差循環を 1 本の式で表現できる
  • 上昇下降が対等ではなく, 下降流が強い: ダウンワードコントロール

線形化した準地平流近似による波の力学

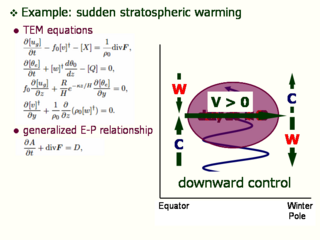
例:成層圏突然昇温
  • 物事の理解に TEM を利用している
  • dA/dt > 0 (観測)
    --> divF < 0 (wave activity の式)
    --> dU/dt < 0 (運動方程式)
    --> V > 0 (運動方程式)
    --> 循環が生じる(連続の式) --> 下向きの循環が強い: ダウンワードコントロール
  • 非線形項は落としても良いくらい小さいのかは疑問がある
    • QG な世界なら大振幅の式自体は問題なく変形できる
    • 非加速定理を証明するならば小振幅でなければならない

平均子午面循環に励起される波

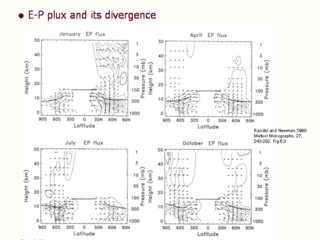
気候学的季節変動 (E-P フラックスとその発散)

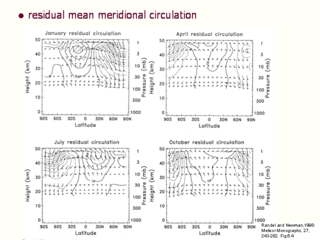
気候学的季節変動 (残差平均子午面循環)
  • divF の大きいところに対応して大きくなる

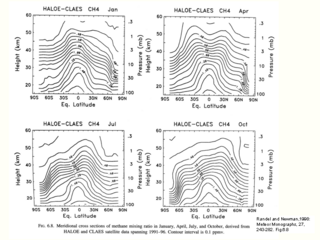
気候学的季節変動 (メタン混合比の子午面断面)
  • 勾配を見ると, 勾配がきつくなり, 緩やかになり, またきつくなる

気候学的季節変動 (子午面平均温度場)
  • 南北の温度差は, 下降流の強弱で理解している
    • そもそもは divF の違い
    • 波のアクティビティが北半球と南半球では異なる
  • 上に向かう波の活動度の原因は
    • ストームトラックの偏在
    • 山岳の有無
    • ストームトラックの偏在

平均子午面循環の模式図

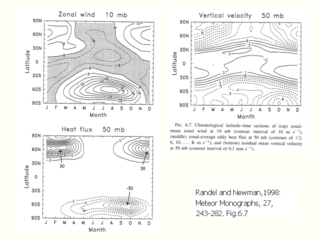
気候学的季節変動 (各物理量の子午面平均緯度時間断面)
  • planetaly 波の活動度が南極, 北極で異なる

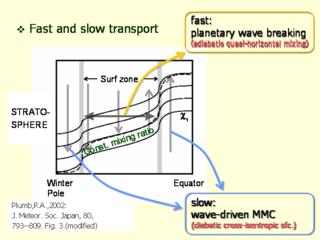
速い輸送と遅い輸送

速い準水平混合に関する数値実験

おしまい

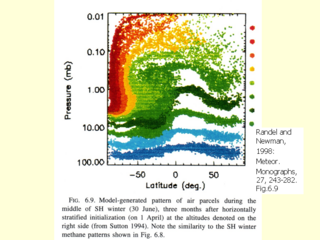
トレーサ実験
  • 中間圏のレオビー循環が見える
  • 南極で下がり, 北極で上昇

参考文献
  • Andrews, D.G., Holton, J.R., Leovy, C.B., 1987: Middle Atmosphere Dynamics. Academic Press, 489pp.
  • Brasseur, G.P., Orlando, J.J., Tyndall, G.S., (Eds.), 1999: Atmospheric Chemistry and Global Change. Oxford University Press, 654pp.
  • Wayne, R.P., 2000: Chemistry of Atmospheres (Third Edition). Oxford University Press, 775pp.
  • Goody, R., 1995: Principles of atmospheric physics and chemistry. Oxford University Press, 324pp.
  • Randel, W.J., Newman, P.A., 1998: The stratosphere in the Southern Hemisphere. In Meteorology of the Southern Hemisphere edited by D. J. Karoly and D. G. Vincent. Meteor Monographs, 27, 243--282.
  • Rossby, C.G., 1939: Relation between variations in the intensity of the zonal circulation of the atmosphere and the displacements of the semi-permanent centers of action. J. Marine Res., 2, 38--55.
  • Ishioka, K., Yamada, M., Hayashi, Y-Y., Yoden, S., 1998: 回転球面上の減衰性2次元乱流からのパターン形成. ながれマルチメディア, http://www.nagare.or.jp/mm/99/ishioka/
  • Charney, J.G., Drazin, P.G., 1961: Propagation of planetary-scale disturbances from the lower into the upper atmosphere. J. Geophys. Res., 66, 83--109.
  • Holton, J.R., 1975: On the influence of boundary layer friction on mixed Rossby-gravity waves. Tellus, 27, 107--115.
  • Andrews, D.G., McIntyre, M.E., 1978: Generalized Eliassen-Palm and Charney-Drazin theorems for waves on axisymmetric mean flows in comoressible atmosphere. J. Atmos. Sci.,35, 175--185.
  • McIntyre, M.E., Palmer, T.N., 1983: Breaking planetary weves in the stratophere. Nature, 305, 593--600.
  • Juckes, M.N., McIntyre, M.E., 1987: A high-resolution one-layer model of breaking planetary waves in the stratosphere. Nature, 328, 590--596.
  • Shepherd, T.G., 2002: Issues in stratosphere-troposphere coupling. J. Meteor. Soc. Japan, 80, 769--792.
  • Plumb, R. A., 2002: Stratospheric transport. J. Meteor. Soc. Japan, 80, 793--809.
  • Mizuta, R. Yoden, S., 2001: 成層圏極渦を想定した準周期流におけるカオス的混合と輸送障壁. ながれマルチメディア, http://www.nagare.or.jp/mm/2001/mizuta/

SUGIYAMA Ko-ichiro 2004-09-22