/地球流体セミナー
/講演資料一覧
/2005-03-17/
原始惑星円盤の安定性について
稲葉知士
2005 年 3 月 17 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|

|
自己紹介
|

|
カーネギー研究所の風景
赤矢印が講演者
|

|
ワシントン D.C.
ホワイトハウスとスミソニアン博物館
|

|
マルセイユ天文台
トランジット法を用いて系外惑星を探す探査衛星を計画.
|
|
マルセイユの風景
(右下) 3 F が滞在中の部屋, 1 F はピザハウス
|
|
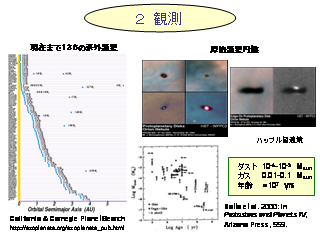
系外惑星の数
- 現在までに 136 個の系外惑星が発見される
- 複数の惑星を持つ場合もある
- 惑星の公転による恒星の摂動を用いて検出する
- トランジット法(惑星が恒星の前面を通過することによる減光を観測)
原始惑星系円盤
- 平たい構造を持つ, 円盤の厚さ/半径 = 1/10
- 円盤に含まれるダストは円盤の年齢(中心星の年齢)がある程度大きくなると急減する
- 中心星の年齢は HR 図上で見積もる
- ダストはミクロンサイズのシリケイト, 氷の粒
|
|
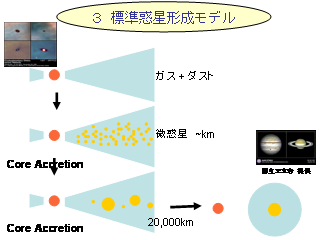
標準惑星形成モデル
- 最初と最後は観測されているので, 途中の進化のシナリオを考えたい
- 1. 円盤は最初ガスとダストの混合物からなる
- 2. ダストが円盤面に沈澱, 集積して km サイズの微惑星を形成
- 3. 特定の微惑星が暴走的に成長, 原始惑星を形成
- 4. 原始惑星があるサイズを越えると円盤ガスを捕獲, ガス惑星となる
|

|
標準惑星形成モデルにおける問題
- 微惑星は形成されるか?
- 円盤面に沈澱したダストが回転軸方向のガスのシアーにともない巻き上げられてしまい, 重力不安定(ジーンズ不安定)が起こらないかもしれない, という懸念
- m サイズまで成長すると, シアーによる巻き上げは効かない.
ただし, ガス抵抗を受けて中心星に落下する時間スケールは 1,000 年程度.
- 今回は 2 の問題について
|

|
原始惑星系円盤進化の記述
- ダストのエネルギーの式は解いていない
- ダスト自身は温度 0 の流体として扱う
- ダストとガスとの間の熱交換は考えない
|
|
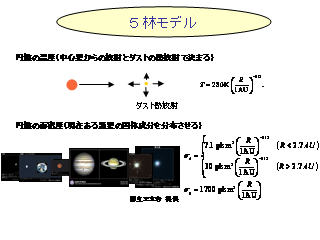
林モデル
- 氷の昇華温度にまで温度が下る 2.7 AU でダスト面密度を増やす.
- ダスト面密度の半径依存性は適当に仮定.
|
|
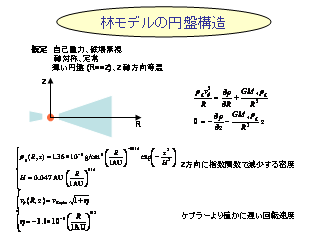
林モデルの円盤構造
ガスの密度と速度分布
- これは z=0 における解
- ちゃんと解くと Vφ には z 依存性がある
(R 方向の温度勾配にともなうシアー).
- 面密度の進化に関する多くの議論, 計算では z 方向の構造を無視してしまう.
|
|
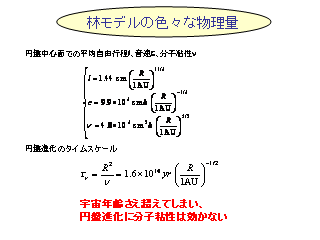
林モデルのいろいろな物理量
- 分子粘性の時間スケールは一般的な円盤進化の時間スケールによりも十分大きい
|
|
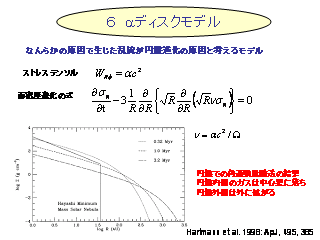
α ディスクモデル
- ガス密度の時間発展を考える.
- 簡単な表現による乱流粘性を導入する, 速度のスケールは音速.
|
|
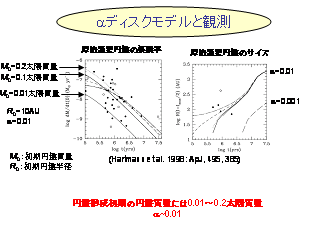
α ディスクモデルと観測との比較
α ディスクモデルの結果
- 最初はケプラー速度で回転している(中心星に近いほど速く回転)
- 乱流粘性により, 内側から外側へ角運動量を輸送
- 内側のガスは中心星方向へ落下し, 外側のガスは中心星からどんどん離れて行く.
|
|
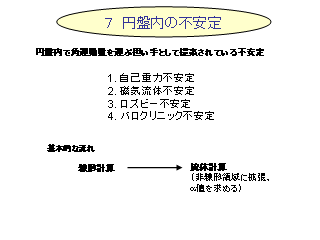
円盤内のガスの不安定
実際の α の値を求める
|

|
自己重力不安定
- ガスが自分の圧力で自分の重力を支えられなくなると発生する不安定,
慣性不安定に自己重力効果を考慮したものと考えればよい.
- 圧力と重力の比で評価
- κ = 1/r3 d(r2Ω)2/dr
= 4Ω2 + 2Ω d&Omega/dr r,
ケプラー運動の場合 κ = Ωk
- κ は角運動量の r 方向勾配による安定化効果を表す.
|

|
自己重力不安定の数値計算
- 重い円盤を初期に置き, 非軸対象な擾乱(波数 2 のモードだけ)を与えて計算.
- 円盤内で Q=1 となるような場所で不安定が起こっていることから,
自己重力不安定であると判断している.
重力定数を 0 にするとこの不安定は現れない.
- 成長率は角度方向波数が小さいと大きい.
自己重力は波長が長いほど大きく, 圧力勾配は波長が短いほど大きいため.
- m=1 は中心星と円盤全体との振動, m=2 は Q < 1,5 で不安定.
- 不安定の発生領域ではガスの質量が増加している.
|
|
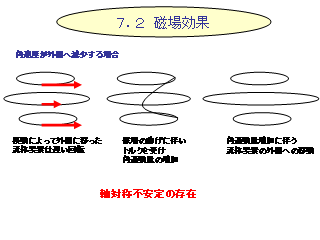
磁場効果
|
|
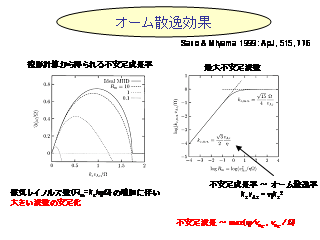
線形安定性解析の結果
- 高波数では安定, 磁力線の張力が強すぎてしまうため.
|
|
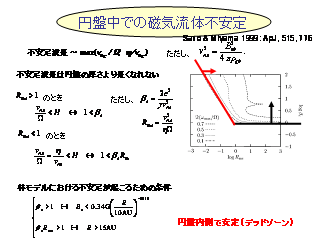
線形安定性解析の結果: 円盤の厚みを考慮した場合
|
|
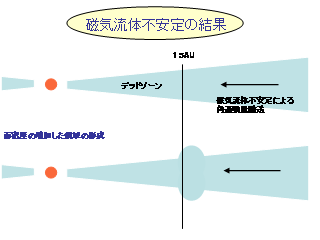
線形安定性解析の結果: 円盤の厚みを考慮した場合
- 角運動量は外側へ, 質量は内側へ輸送
- 15 AU 付近で質量がたまる
|

|
ロスビー不安定
- 磁気流体不安定によって生じた質量のたまり場で, 別種の不安定が生じるかどうかを考える.
- 順圧不安定 (?)
- 擾乱の分散関係がロスビー波に似ている
- 低周波成分だけをとりだすため, ω2 の項(=音波成分?)を無視する近似を行っている.
- Lovelace et al. (1999) の分散関係をよくみると…
- 短波長極限:
不安定となる場合は浮力振動数が負の場合 = 対流不安定.
L(R) の勾配がなくても不安定が起こる. 順圧不安定ではない?
- 長波長極限:
ロスビー波と ω=0 のモード
- 不安定の条件 (L(R)が極値を持つ) は順圧不安定の場合の不安定条件とよく似ている. WKB 近似での議論ではなく波の相互作用を用いた議論をすべきでは?
- Li et al. (2001) では積分形式で不安定性を議論し, 対流不安定ではない不安定が存在することを示している(らしい).
|
|
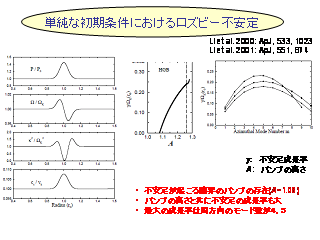
単純な初期条件におけるロスビー不安定
- Ls=∞ の場合 (エントロピー一定).
対流不安定は起こらない条件での線形解析.
- これは正しいロスビー不安定 ?
|
|
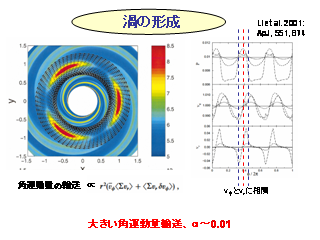
渦の形成
- 非線形の計算 (Ls=∞ の場合, エントロピー一定).
- m=3 の初期擾乱を与える
- 磁気流体不安定の起こらない領域でも角運動量輸送が起こり得ることを示した.
|
|
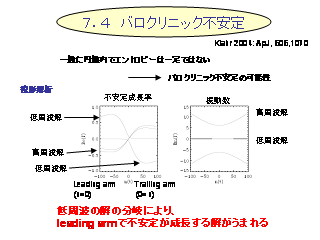
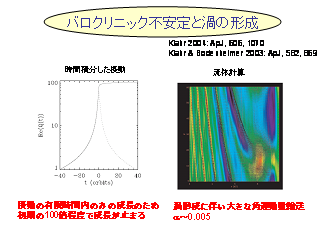
バロクリニック不安定
- 動径方向にエントロピー勾配がある場合.
- 分散関係は ω の 4 次式になる, 音波と重力波(ロスビー波と分離できない)
- Leading arm: ケプラー速度と同方向に螺旋をまく渦
- Trailing arm: ケプラー速度と逆方向に螺旋をまく渦
- 最初 Leading arm な渦は引き延ばされて Trailing arm な渦になる.
有限時間内でしか不安定にならない.
これは気象学で言うところのバロクリニック不安定?
- たぶん違う.
- 渦が流される解. 振幅は線形成長. 指数的に増幅する解ではない
- Orr の解と類似のもの?
|
|
バロクリニック不安定と渦の形成
- (左) 線形計算
- (右) 非線形計算, こちらの計算が先に行われた. 基本場のガス密度は一定.
|
|
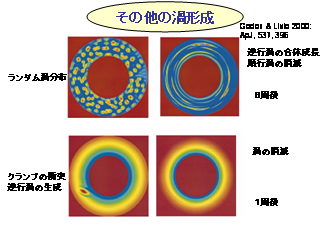
その他の渦の数値計算
|
|
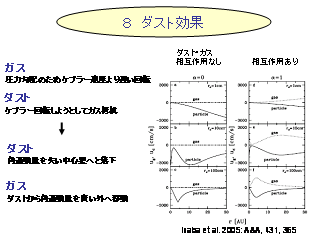
ダスト効果
|

|
ダスト移動にともなうガス面密度の進化
- ダストがガスと同程度存在する場合
- ダストからガスへの角運動量輸送を考慮すると, ダストの中心星への落下が抑制され, ガスは外側へ輸送される.
|
|
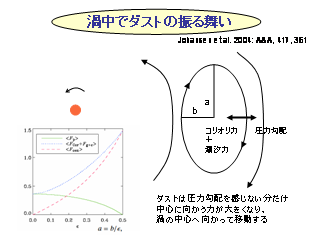
渦中でのダストの振る舞い
|
|
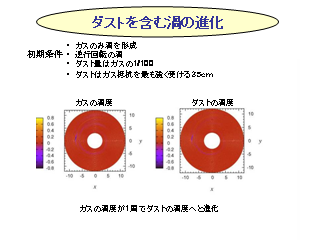
ダストを含む渦の進化
|
|
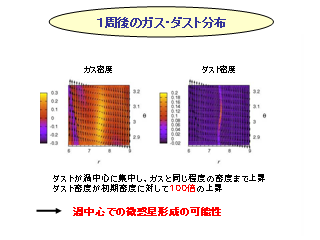
1 周後のガス・ダスト分布
|
|
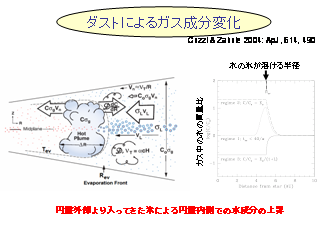
ダストによるガス成分の変化
- 氷が解ける温度を持つ半径を境に, 外側では水はダスト, 内側では蒸気として存在.
- 円盤外側で形成された氷微惑星の中心星への落下が速い場合を想定.
子午後面循環(?)は考えなくてよい?
- 地球大気では, 地表摩擦があることで子午面循環がおこる.
- 赤道面にたまったダストによるガスへの摩擦は,
地球大気における地表摩擦と同じ役割を果たすのではないか?
|

|
まとめ
|
参考文献
-
Beckwith, S. V. W., Sargent, A. I., Chini, R. S., Guesten, R., 1990:
A survey for circumstellar disks around young stellar objects.
The Astronomical Journal, 99, 924--945.
- Binney, J., & Tremain, S. 1987, Galactic dynamics.
- Boss, A. P., 1997:
Giant Planet Formation by Gravitational Instability.
Science,
276, 1836--1839.
- * Brandenburg, A., Nordlund, A., Stein, R. F., & Totkelsson, U. 1995, ApJ, 446, 741
- Blubus, S. A., Hawley, J. F., 1998:
Instablity, turbulence, and enhanced transport in accretion disks.
Rev. Mod. Phys.,
70, 1--53.
- Cuzzi, J. N., Zahnle, K. J., 2004:
Material Enhancement in Protoplanetary Nebulae by Particle Drift
through Evaporation Fronts.
Astrophys. J.,
614, 490--496.
- Godon, P., Livio, M., 2000:
The Formation and Role of Vortices in Protoplanetary Disks.
Astrophys. J.,
537. 396--404.
- Hartmann, L., Calvet, N., Gullbring, E., D'Alessio, P., 1998:
Accretion and the Evolution of T Tauri Disks.
Astrophys. J.,
495, 385--400.
- Hayashi, C., Nakazawa, K., Nakagawa, Y., 1985:
Formation of the solar system.
in Protostars and Planets II, Arizona Press, 1100--1153.
- Inaba, S., Barge, P., Daniel, E., Guillard, H., 2005:
A two-phase code for protoplanetary disks.
Astronomy and Astrophysics,
431, 365--379.
- Johansen, A., Andersen, A. C., Brandenburg, A., 2004:
Simulations of dust-trapping vortices in protoplanetary discs.
Astronomy and Astrophysics,
417, 361--374.
- Klahr, H., 2004:
The Global Baroclinic Instability in Accretion Disks. II.
Local Linear Analysis.
Astrophys. J.,
606, 1070--1082.
- Klahr, H., Bodenheimer, P., 2003:
Turbulence in Accretion Disks: Vorticity Generation and
Angular Momentum Transport via the Global Baroclinic Instability.
Astrophys. J.,
582, 869--892.
- Li, H., Finn, J. M., Lovelace, R. V. E., Colgate, S. A., 2000:
Rossby Wave Instability of Thin Accretion Disks. II.
Detailed Linear Theory.
Astrophys. J.,
533, 1023--1034.
- Li, H., Colgate, S. A., Wendroff, B., Liska, R., 2001:
Rossby Wave Instability of Thin Accretion Disks. III.
Nonlinear Simulations.
Astrophys. J.,
551, 874--896.
- Laughlin, G., Bodenheimer, P., 1994:
Nonaxisymmetric evolution in protostellar disks,
Astrophys. J.,
436, 335--354.
- Lovelace, R. V. E., Li, H., Colgate, S. A., Nelson, A. F., 1999:
Rossby Wave Instability of Keplerian Accretion Disks.
Astrophys. J.,
513, 805--810.
- Natta, A., Grinin, V. P., Manings, V. 2000:
Properties and Evolution of Disks Around Premain-Sequence Stars of
Intermediate Mass.
Protostars and Planets IV,
ad. V.Mannings, A. P. Boss, and S. S. Russel,
University of Arizona Press, 559--589.
- Pringle, J. E., 1981:
Accretion Discs in Astrophysics.
Ann. Rev. Astron. Astrophys., 19, 137--160.
- Sano, T., Miyama, S. M., 1999:
Magnetorotational Instability in Protoplanetary Disks. I.
On the Global Stability of Weakly Ionized Disks
with Ohmic Dissipation
Astrophys. J.,
515, 776--786.
- California & Carnegie Planet Search,
http://exoplanets.org/exoplanets_pub.html
- 国立天文台 すばるギャラリー,
http://subarutelescope.org/Gallery/
Odaka Masatsugu
2005-03-24
|