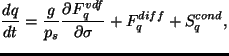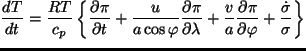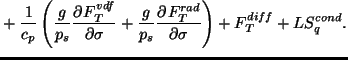: 離散化
: 数値モデルの説明
: 数値モデルの説明
モデルの力学部分は渦度, 発散, 静水圧平衡, 湿度, 熱力学の式からなり
下の方程式となっている.
これらの方程式の中で,
ここで,
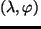 緯度と経度とを表す座標;
緯度と経度とを表す座標;
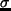 鉛直座標;
鉛直座標;
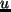 ,
, 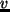 水平風成分;
水平風成分;
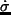 は
は 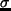 座標系における鉛直速度;
座標系における鉛直速度;
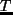 温度;
温度;
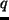 比湿;
比湿;
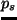 地表面気圧;
地表面気圧;
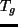 地表面温度;
地表面温度;
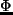 ジオポテンシャル;
ジオポテンシャル;
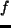 コリオリパラメータ;
コリオリパラメータ;
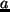 地球半径;
地球半径;
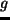 重力加速度;
重力加速度;
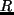 乾燥空気の気体定数;
乾燥空気の気体定数;
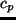 大気の定圧比熱;
大気の定圧比熱;
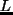 水の潜熱;
水の潜熱;
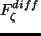 ,
, 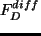 ,
, 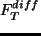
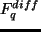 水平拡散項;
水平拡散項;
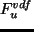 ,
, 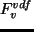 ,
, 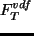 ,
,
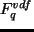 鉛直拡散項;
鉛直拡散項;
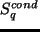 is 比湿の凝結源である.
is 比湿の凝結源である.
水平拡散項は
超粘性タイプ(hyper-viscosity type)の公式で次のように与えられる,
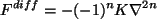 |
(12) |
ここでは 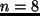 としている.
としている.
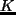 の値は波数 42 の成分の減衰時間が 4 時間となるように決めている.
の値は波数 42 の成分の減衰時間が 4 時間となるように決めている.



: 離散化
: 数値モデルの説明
: 数値モデルの説明
okuyama naonori
平成13年1月10日
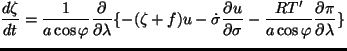
![$\displaystyle \qquad - \frac{1}{a \cos \varphi}
\DP{}{\varphi}
[ \{ (\zeta + f)...
...{\sigma}
- \frac{RT'}{a} \DP{\pi}{\varphi} \} \cos \varphi]
- F^{diff}_{\zeta},$](img2.gif)
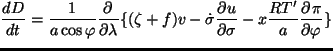
![$\displaystyle \qquad + \frac{1}{a \cos \varphi} \DP{}{\varphi}
[ \{ (\zeta + f)...
... \dot{\sigma} \DP{u}{\sigma}
- \frac{RT'}{a} \DP{\pi}{\varphi} \} \cos \varphi]$](img4.gif)