渦度場 (統計的平衡状態, スナップショット)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均東西速度 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均東西速度 (統計的平衡状態, スナップショット)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均渦度 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均渦度 (統計的平衡状態, スナップショット)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均渦度の南北微分 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均渦度の南北微分 (統計的平衡状態, スナップショット)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
エネルギーの時系列, E(t)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
エンストロフィーの時系列, Z(t)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
パリンストロフィーの時系列, P(t)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均エネルギーの時系列, E_z(t)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均エンストロフィーの時系列, Z_z(t)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
帯状平均パリンストロフィーの時系列, P_z(t)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
エネルギー散逸率の時系列

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
エンストロフィー散逸率の時系列

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
エネルギースペクトル (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15
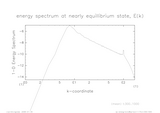
beta = 20

beta = 25

beta = 30
1次元エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
エネルギーフラックス (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
位相シフト (統計的平衡状態, 時間平均, 緯度平均)







2次元エネルギースペクトル (統計的平衡状態, スナップショット)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギースペクトル (統計的平衡状態, スナップショット, 拡大その1)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギースペクトル (統計的平衡状態, スナップショット, 拡大その2)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギースペクトル (統計的平衡状態, スナップショット, 拡大その3)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギースペクトル (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギースペクトル (統計的平衡状態, 時間平均, 拡大その1)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギースペクトル (統計的平衡状態, 時間平均, 拡大その2)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギースペクトル (統計的平衡状態, 時間平均, 拡大その3)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギー輸送 (統計的平衡状態, 時間平均, 拡大その1)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギー輸送 (統計的平衡状態, 時間平均, 拡大その2)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
2次元エネルギー輸送 (統計的平衡状態, 時間平均, 拡大その3)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化1次元エネルギー輸送 (統計的平衡状態, 時間平均)







粗視化1次元エネルギー輸送フラックス (統計的平衡状態, 時間平均)







低波数の波二つから高波数の波への正味エネルギー輸送 (統計的平衡状態, 時間平均)







高波数の波二つから低波数の波への正味エネルギー輸送 (統計的平衡状態, 時間平均)







粗視化領域 0 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 1 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 2 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 3 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 4 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 5 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 6 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 7 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 8 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 9 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 10 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 11 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 12 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 13 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
粗視化領域 14 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
スケール分離パラメタによって分類された波数0のエネルギー輸送フラックス (統計的平衡状態, 時間平均)
スケール分離パラメタによって分類された波数1のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数2のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数3のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数4のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数5のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数6のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数7のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数8のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数9のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数10のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数11のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数12のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数13のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数14のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数15のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された波数16のエネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数0より小さい波数の波二つから0より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数1より小さい波数の波二つから1より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数2より小さい波数の波二つから2より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数3より小さい波数の波二つから3より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数4より小さい波数の波二つから4より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数5より小さい波数の波二つから5より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数6より小さい波数の波二つから6より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数7より小さい波数の波二つから7より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数8より小さい波数の波二つから8より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数9より小さい波数の波二つから9より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数10より小さい波数の波二つから10より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数11より小さい波数の波二つから11より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数12より小さい波数の波二つから12より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数13より小さい波数の波二つから13より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数14より小さい波数の波二つから14より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)
スケール分離パラメタによって分類された, 波数15より小さい波数の波二つから15より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)
スケール分離パラメタによって分類された, 波数16より小さい波数の波二つから16より大きい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)
スケール分離パラメタによって分類された, 波数0より大きい波数の波二つから0より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数1より大きい波数の波二つから1より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数2より大きい波数の波二つから2より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数3より大きい波数の波二つから3より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数4より大きい波数の波二つから4より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数5より大きい波数の波二つから5より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数6より大きい波数の波二つから6より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数7より大きい波数の波二つから7より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数8より大きい波数の波二つから8より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数9より大きい波数の波二つから9より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数10より大きい波数の波二つから10より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数11より大きい波数の波二つから11より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数12より大きい波数の波二つから12より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数13より大きい波数の波二つから13より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)







スケール分離パラメタによって分類された, 波数14より大きい波数の波二つから14より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)
スケール分離パラメタによって分類された, 波数15より大きい波数の波二つから15より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)
スケール分離パラメタによって分類された, 波数16より大きい波数の波二つから16より小さい波数の波への正味エネルギー輸送フラックス (統計的平衡状態, 時間平均)
線形Rossby波の振動数で分類した, 粗視化領域 0 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 1 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 2 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 3 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 4 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 5 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 6 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 7 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 8 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 9 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 10 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 11 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 12 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 13 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 14 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 15 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 16 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 17 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30
線形Rossby波の振動数で分類した, 粗視化領域 18 への粗視化エネルギー輸送 (統計的平衡状態, 時間平均)

beta = 0

beta = 5

beta = 10

beta = 15

beta = 20

beta = 25

beta = 30