|
The time integration of 1D thermal conduction equation of ground
surface (A.55)
in appendix A.e is performed by
the Crank-Nicolson scheme.
The space differencing in (A.55) is evaluated by the second
order centered scheme.
The ground temperature and vertical grid interval are evaluated on the
grid point and the heat flux is evaluated on the half grid point.
The number of vertical grid point is 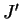 and the suffix
varies and the suffix
varies 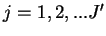 from the lowest grid point.
The from the lowest grid point.
The 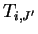 is assumed to the surface temperature is assumed to the surface temperature
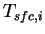
Where 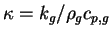 .
When the terms at .
When the terms at 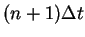 are moved to left hand side
and the terms at are moved to left hand side
and the terms at 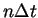 are moved to right hand side, then are moved to right hand side, then
Where 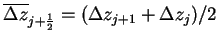 .
When .
When 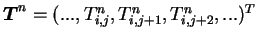 , this equation can be represented in
matrix form as follows. , this equation can be represented in
matrix form as follows.
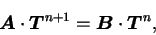 |
(B.61) |
The matrix 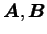 are J'-th order square matrix
and these elements are are J'-th order square matrix
and these elements are
Considering the upper boundary condition
(A.56) and
insurate lower boundary,
(B.61) is modified as follows.
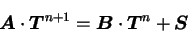 |
(B.62) |
Therefore,
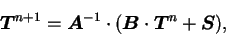 |
(B.63) |
where the first and 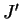 th diagonal element
of th diagonal element
of 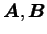 are represented as follows. are represented as follows.
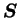 is a column vector whose dimension is is a column vector whose dimension is
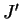 and which elements are represented as follows. and which elements are represented as follows.
|