- 思考実験 : 安定成層, linear な鉛直密度分布.
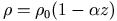
- スプーンでかき混ぜると一様な密度分布になる.
- 与えた運動エネルギーはどうなる? -> 熱エネルギー or 位置エネルギーにかわる.
- かき混ぜ前後の位置エネルギー差を計算
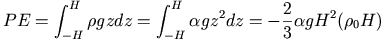
かき混ぜ後は
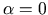 だから
だから 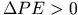 .
位置エネルギーは増えている.
.
位置エネルギーは増えている.
- 効率 = 位置エネルギー増加 / 全エネルギー
-
mixing の室内実験(Park, Whitehead, Gnanadeskian)

- 塩水が成層している状態と水が隣り合っている.
- 棒を一定スピードで動かして乱流を生成する.
- すると塩水境界が wavy になるようすが見られる.
- このような現象はこれまでに説明した Eddy diffusion では 説明できない. diffusion 型モデルでは線形分布の傾きが 弱くなるだけ
-
室内実験 : 密度, 勾配の時間変化

- Is turbulence stable? (Phillips 1972)
- 鉛直密度分布に階段状の構造
- 密度一様な層毎に turbulence が存在. 層間の境界では 安定成層なので乱流が抑えられている.
- 密度勾配のスパイクがだんだんくっついて行く様子が見られる.
-
室内実験 : 密度, 勾配の時間変化その 2

- 密度勾配のスパイクが単に消えて行くだけの場合もある : fade out
-
室内実験 : 密度, 勾配の時間変化その 3

- 密度分布によって全く振舞が異なる.
- 密度分布が重要 :
-
理論

- 密度勾配 g に対するフラックス f の関係
- 密度勾配が弱いと, 一様密度中の渦輸送.
- 密度勾配が強くなると, 成層で乱流が抑えられ, フラックスが減る
- さらに強くなるとやがて分子拡散による輸送が卓越する.
- この f 〜 g=b_z 関係を S-shaped curve と呼ぼう.
-
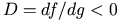 : negative diffusion という.
: negative diffusion という.
この定義は通常の negative difuusion の呼び方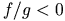 とは
ことなる.
とは
ことなる.
-
p2 モデル
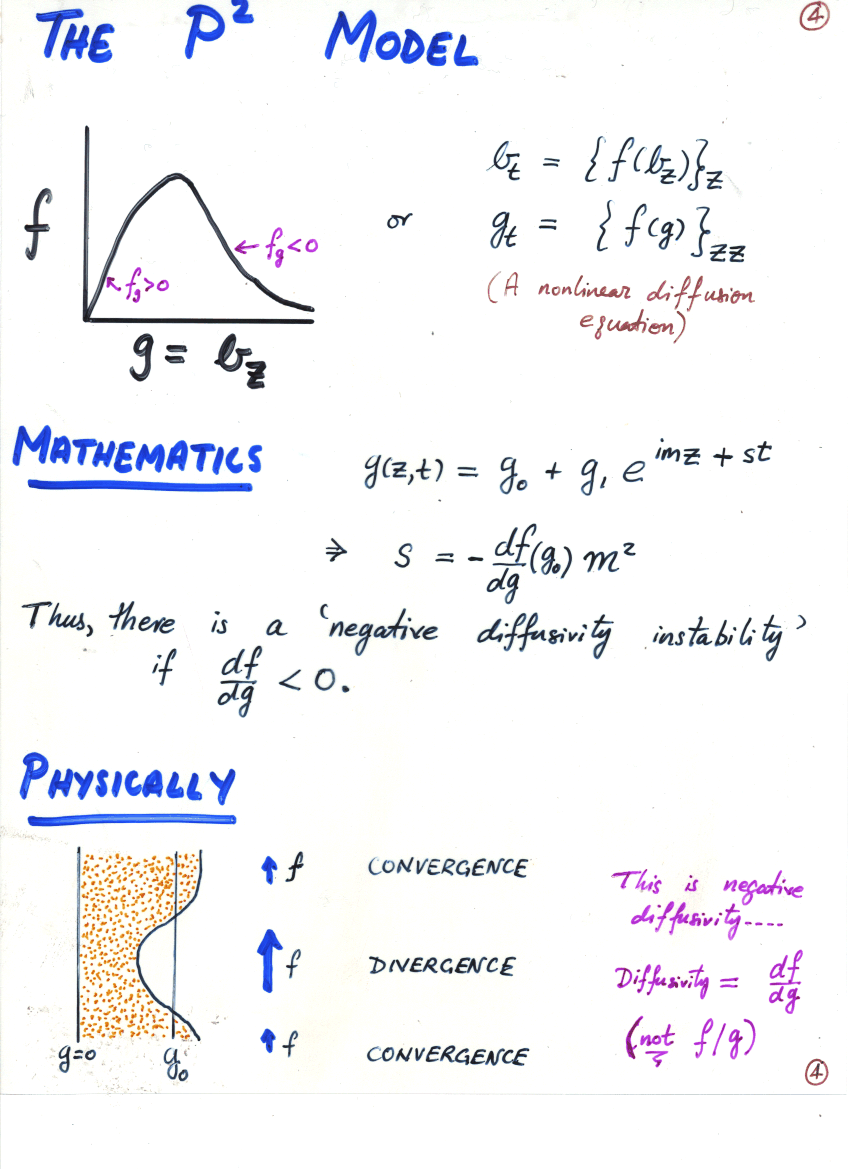
- なぜ f/g でなく df/dg を用いて negative diffusion と称すか?
-
層形成する不安定

- Negative diffusion : df/dg が層形成に重要な要素
-
Negative diffusion の簡単なモデル

- 周期的な強制による流れを考える.
- 浮力のフラックスの極限 : N2 が小さいと, これまでのパッシブトレーサーの拡散. 流れによってフラックスが強化される.
- 浮力のフラックスの極限 : N2 が大きいと分子拡散が効くだけ
- N2が小さいところでの df/dg (拡散係数)が大きいので S 型の f-g 曲線になる.
-
Negative diffusion の簡単なモデル : エネルギー収支

- N2が大きいと注入されたエネルギーが 全て位置エネルギーへ変換される.

-
モデル

- 階段状の層の厚さは?
- 変数を水平方向に平均した量で考える
- mixing length : l の候補は二つ.
Forcing で用いた棒の幅か, 運動エネルギーから作られる 長さスケール. - このうち小さい方をとるべし.
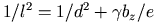
-
モデル : mixing length を用いた表現

- スケーリング, 次元解析からエネルギー方程式を構成する.
- Production term をのぞいて系が閉じている.
-
モデル : 生成項の与え方

-
P の与え方による Flux-gradient 関係

- e = constant(定常, 一様), g = constant (定常, 一様)として 先のモデルを解いた結果.
-
The Equipartition model for P

-
数値計算結果

- スパイクが merge して行く
-
数値計算結果 : flux-gradient 関係

-
数値計算結果 : spike の時間変化

- スパイクが merge して行くだけでなく, 消えていくものもある.
-
室内実験, シミュレーション

- シミュレーションに見られるフラックス時間変化の一定領域の 三角形は, mixing length model のスパイクの merge の様子と 似ている
-
スパイクの merging の様子

-
結論

