/地球流体セミナー
/講演資料一覧
/2003-09-08/
シアー不安定の基礎:
シアー不安定の数学的な取り扱い(固有値問題)
伊賀 啓太(九大・応用力学研究所)
2003 年 9 月 9 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|

|
目次
|

|
タイトルページ
|

|
流れの安定・不安定
解に微小な擾乱を加えた時に,
- 時間とともに解が元の状態から離れていく : 不安定
- 時間とともに解が元の状態へ戻っていく : 安定
|

|
例題: 階段関数状の流れ
(図は流線関数の分布)
- y=0 付近に擾乱を与えると渦が発生する.
- 元の流れ場とは異なる流れ場が現れる : 不安定
|

|
流れの不安定の数学的取扱
線形安定論
- 定常な基本場 + 微小振幅の擾乱場に分ける
- 擾乱の 2 次以上の項は無視する
|

|
流れの不安定の数学的取扱
線形安定論 (つづき)
|

|
2 次元, 基本場が平行流の場合
- 基本場の流れ方向を x, それと垂直な方向を y とする.
- U = (U(y),0), f = f(y), β = df/dy
擾乱も 2 次元で考える
- f=0 の場合, 同じ全波数であれば m=0 のモードの成長率が最大.
(Squire の定理)
- 数学的な解説は Drazin and Reid (1981), p129 を見よ.
- f=0 でない場合は…?
|

|
渦位方程式の導出
|

|
線形化された渦位方程式
|

|
擾乱を波形の解と仮定する
Reyleigh 方程式
|

|
問題の解法
y = 0, 1 で φ = 0 という境界条件を考えると…
- 適当な任意の c に対する解は自明な解 (φ = 0).
- 自明でない解は, 係数行列の固有値問題を解くことによって得られる.
|

|
粘性がない場合,
- Im(c) > 0 の解と Im(c) < 0
の解は対になって現れる.
- Rayleigh 方程式を見ると, 固有値 c に対する解 φ があると,
固有値 c* に対する解は φ* であることがわかる.
|
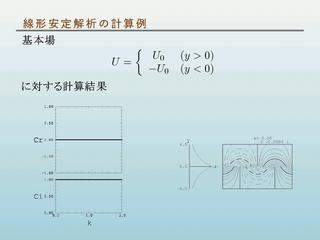
|
計算例: 基本場に階段関数状の速度分布与えた場合
- 左図 : 固有値(位相速度と成長率)
- 虚数部は正の部分だけ表す. 負の部分は k 軸に対し対称な位置にある.
- 右図 : 擾乱の固有関数
- y = 0 で不連続
- U が y = 0 で不連続なため.
この他に連続モード解がある.
- U0 または -U0 で流される解
- 振幅は y > 0 または y < 0 にのみ存在.
|
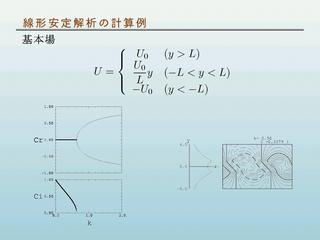
|
計算例: 速度の不連続をなくした場合
|
|
|
参考文献
- Drazin, P. G., and W. H. Reid, 1981:Hydrodynamic stability,
Cambridge Univ. Press, pp. 527.
|
Odaka Masatsugu
2003-09-09
|














