The space differencing in the turbulent kinetic energy equation
(equation (10) in Part I) is evaluated by the forth
order centered scheme for advection terms and the second order
centered scheme for other terms.
In time integration, the forward scheme is adapted for the
friction terms.
Representations of
![]() and
and
![]() are same as those of
(22) and (24).
are same as those of
(22) and (24).
![$\displaystyle + \left.
[\mbox{DKBP}]_{i,j}^{n} +
[\mbox{DKSP}]_{i,j}^{n} -
\frac{C_{\epsilon}}{l}(\varepsilon _{i,j}^{N})^{\frac{3}{2}} \right\}$](img147.png) |
(41) |
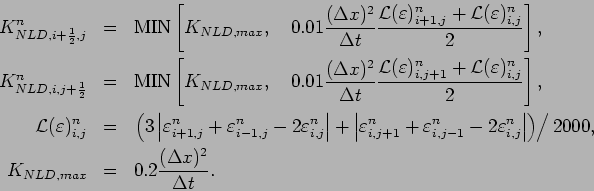
![$\displaystyle -\frac{g}{\Theta _{0,j}}K_{i,j}^{n}
\frac{1}{\Delta z_{j}}\left[
...
...+\frac{1}{2}}) -
(\theta _{i,j-\frac{1}{2}}+\Theta _{0,j-\frac{1}{2}}) \right],$](img153.png) |
(43) | ||
![$\displaystyle 2K_{i,j}^{n}\left[
\left(
\frac{u_{i+\frac{1}{2},j}^{n}-u_{i-\fra...
...i,j+\frac{1}{2}}^{n}-w_{i,j-\frac{1}{2}}^{n}}{\Delta z_{j}}
\right)^{2}
\right]$](img155.png) |
|||
![$\displaystyle + \frac{2}{3}\varepsilon _{i,j}^{n} \left[
\frac{u_{i,j+\frac{1}{...
..._{j}} +
\frac{w_{i+\frac{1}{2},j}^{n}-w_{i-\frac{1}{2},j}^{n}}{\Delta x}\right]$](img156.png) |
|||
![$\displaystyle + K_{i,j}^{n}
\left[
\frac{u_{i,j+\frac{1}{2}}^{n}-u_{i,j-\frac{1...
...} +
\frac{w_{i+\frac{1}{2},j}^{n}-w_{i-\frac{1}{2},j}^{n}}{\Delta x}\right]^{2}$](img157.png) |
(44) |
The finite difference form of the surface flux are as follows.
| (45) | |||
| (46) |
where
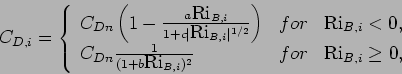 |
(47) |
The bulk Richardson number is calculated as follows.
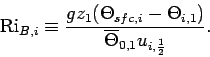 |
(48) |