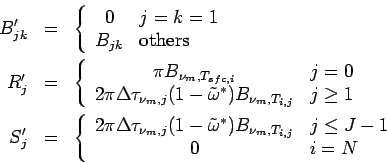The radiative heating rate is calculated from the radiative flux by
using the second order centered scheme.
| (51) | |||
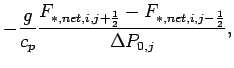 |
(52) |
The radiative flux is evaluated on the half grid point
The subscript ![]() shows grid point in the wave number.
In the following sections, the superscript which shows time step is omitted.
shows grid point in the wave number.
In the following sections, the superscript which shows time step is omitted.
The finite difference form of the infrared radiative flux
and the Plank function are represented as follows.
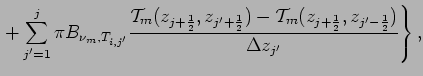 |
(53) | ||
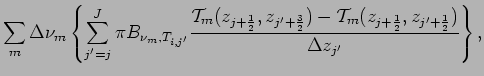 |
(54) | ||
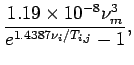 |
(55) | ||
| (56) |
where the averaged transmission function, the equivalent width, and the effective path length are represented as follows.
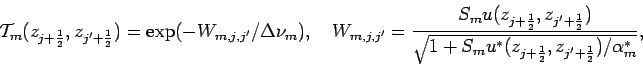
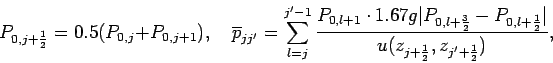
The finite form of the near infrared radiative flux
and the effective path length are represented as follows.
| (57) |
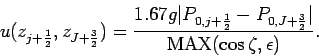
where ![]() is a small parameter to ensure
is a small parameter to ensure
![]() when
when ![]() .
.
The finite difference form of the solar radiative transfer equation of dust
are represented as follows.
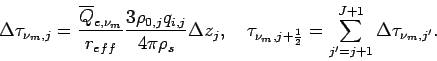
(58) and
(59)
can be represented in matrix form as follows.
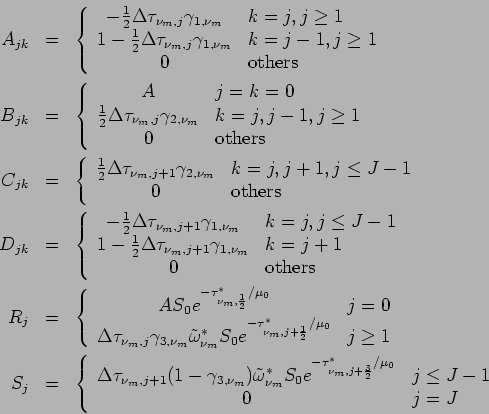
The finite difference form of the solar radiative transfer equation of dust
are represented as follows.
(62) and
(63)
can be represented in matrix form as follows.