|
ダストによる太陽放射, 赤外放射の吸収, 散乱, 射出はともに
δ-Eddington 近似 (例えば
Liou, 1980 を参照)を用いて計算する. δ-Eddington
近似は非等方な散乱のある大気放射伝達を計算する場合によく用いられる方法である.
可視光および赤外光に対するダストの非対称因子はともに前方散乱を表す
0 から 1 の範囲にある
(付録 A.d.v 節 参照).
ダストによる太陽放射の散光の上向き放射フラックス
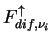 , 下向き放射フラックス , 下向き放射フラックス
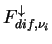 は以下の式で計算される.
は以下の式で計算される.
境界条件は, 大気上端での下向き放射
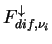 が 0,
大気下端での上向き放射 が 0,
大気下端での上向き放射
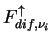 は は
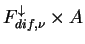 ( (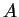 は地表面アルベド) である. は地表面アルベド) である.
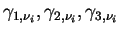 はそれぞれ はそれぞれ
と表される.
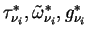 は δ-Eddington 近似に伴い修正された光学的厚さ,
一次散乱アルベド, 非対称因子で, それぞれ は δ-Eddington 近似に伴い修正された光学的厚さ,
一次散乱アルベド, 非対称因子で, それぞれ
である.
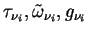 はもともとの光学的厚さ, 一次散乱アルベド, 非対称因子である.
はもともとの光学的厚さ, 一次散乱アルベド, 非対称因子である.
ダストによる赤外放射の吸収と散乱, 射出も同様に計算する.
ただし太陽直達光の一次散乱を表す項の代わりに熱輻射項が付く.
境界条件は, 大気上端での下向き放射
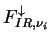 が 0,
大気下端での上向き放射 が 0,
大気下端での上向き放射
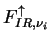 は は
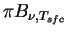 である.
(A.33),
(A.34)
式中のプランク関数 である.
(A.33),
(A.34)
式中のプランク関数
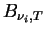 は, バンド内での平均値を用いる. は, バンド内での平均値を用いる.
ここで
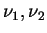 は各バンドの上端と下端の波長である. は各バンドの上端と下端の波長である.
ダスト放射による放射加熱率は以下の式で計算される.
ここで
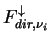 は直達太陽放射フラックスで, は直達太陽放射フラックスで,
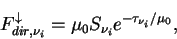 |
(A.37) |
である.
考慮する波長領域と光学パラメータは
Forget et al. (1999) のそれに準じている.
Forget et al. (1999)
では CO2 の 15 μm バンドと重なる 11.6-20 μm
バンドを考慮しているが, 本研究では考慮しない.
吸収線が重なる場合の放射伝達の扱いが多少複雑になるからである.
可視光波長領域バンドと CO2
近赤外吸収帯との吸収線の重なりは無視する.
CO2 によって吸収される太陽放射量は全太陽放射量の 1% 程度なので,
吸収線の重なりを無視しても放射計算の結果は変わらないと判断したからである.
太陽放射に対する消散効率
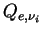 は
Ockert-Bell, et al. (1997)
における 0.67 μm の値 (3.04) を用いる.
赤外波長域の光学的厚さに対する可視波長域の光学的厚さの比は
Forget (1998) に従い 2 とする.
考慮する波長帯とダストの光学パラメータの詳細は
付録 A.d.v 節 に示した. は
Ockert-Bell, et al. (1997)
における 0.67 μm の値 (3.04) を用いる.
赤外波長域の光学的厚さに対する可視波長域の光学的厚さの比は
Forget (1998) に従い 2 とする.
考慮する波長帯とダストの光学パラメータの詳細は
付録 A.d.v 節 に示した.
ダストの質量混合比から光学的厚さを求めるためには, ダストの有効半径
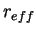 が必要となる.
有効半径はダストの粒径分布から計算される
(付録 A.d.iv 節 参照).
本研究ではダストの粒径分布として
Toon et al. (1977) で用いられた変形ガンマ関数分布を仮定する. が必要となる.
有効半径はダストの粒径分布から計算される
(付録 A.d.iv 節 参照).
本研究ではダストの粒径分布として
Toon et al. (1977) で用いられた変形ガンマ関数分布を仮定する.
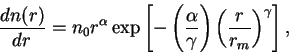 |
(A.38) |
ここで
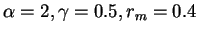 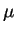 m とする. このとき有効半径
は 2.5 μm
(Pollack et al., 1979) となる. m とする. このとき有効半径
は 2.5 μm
(Pollack et al., 1979) となる.
|