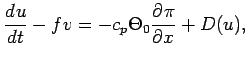 |
(1) | ||
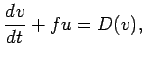 |
(2) | ||
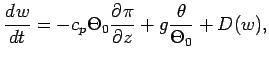 |
(3) | ||
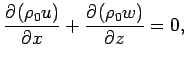 |
(4) | ||
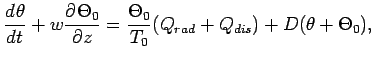 |
(5) | ||
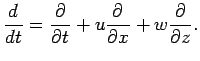 |
The governing equation of model atmospheric dynamics is the 2D anelastic system (Ogura and Phillips, 1962).
(1), (2), (3)
are the horizontal and
vertical component of equation of motion, respectively.
(4) is the continuity equation
and (5) is the thermodynamic equation.
![]() are horizontal, vertical and time
coordinate, respectively.
are horizontal, vertical and time
coordinate, respectively.
![]() are horizontal and vertical velocity, and
are horizontal and vertical velocity, and
![]() are potential temperature and
nondimensional pressure function deviation from those of basic
state, respectively.
are potential temperature and
nondimensional pressure function deviation from those of basic
state, respectively.
![]() are density, potential temperature and
temperature in basic state.
are density, potential temperature and
temperature in basic state.
![]() is gravitational acceleration whose value
is equal to 3.72 msec
is gravitational acceleration whose value
is equal to 3.72 msec![]() .
.
![]() is radiative heating (cooling) rate per
unit mass which is calculated by convergence of the radiative heat flux.
is radiative heating (cooling) rate per
unit mass which is calculated by convergence of the radiative heat flux.
![]() is heating rate per unit mass owing to
dissipation of turbulent kinetic energy, which is given by
turbulent parameterization.
is heating rate per unit mass owing to
dissipation of turbulent kinetic energy, which is given by
turbulent parameterization.
![]() term in equation (1)
term in equation (1)![]() (5)
represents the turbulent diffusion owing to subgrid scale turbulent
mixing.
(5)
represents the turbulent diffusion owing to subgrid scale turbulent
mixing.
![]() is turbulent diffusion coefficient which
is calculated by
(10) and (11).
is turbulent diffusion coefficient which
is calculated by
(10) and (11).
The nondimensional pressure function and potential temperature are
defined as follows.
The model horizontal boundary is cyclic. The vertical wind velocity is set to be 0 at the surface and upper boundary.
| Parameters | Standard Values | Note |
| 0 sec |
||
| 3.72 msec |
||
| 7 hPa | ||
| 734.9 Jkg |
Value of CO |
|
| 189.0 Jkg |
Value of CO |