

Next: ブジネスク近似
Up: スベルドラップ・バランス
Previous: スベルドラップ・バランス
海洋の運動は大気の運動と同様にナビエ・ストークスの方程式で記述される.
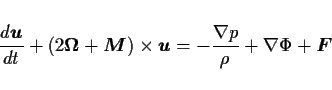 |
(1) |
ここで
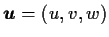 は流速ベクトル,
は流速ベクトル,
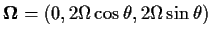 は地球の角速度
ベクトル,
は地球の角速度
ベクトル,
 はメトリック項,
はメトリック項,  は緯度, r は地球中心からの距離, p は圧力,
は緯度, r は地球中心からの距離, p は圧力, 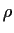 は密度,
は密度,  はポ
テンシャル(たとえば重力ポテンシャル), また d/dt は以下の通りである.
はポ
テンシャル(たとえば重力ポテンシャル), また d/dt は以下の通りである.
ここで  は経度を表す.
は経度を表す. 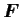 は粘性やその他の外力を表
す. いま特に外から与えられる物体力がない場合,
は粘性やその他の外力を表
す. いま特に外から与えられる物体力がない場合,
 は次のように表される.
は次のように表される.
AM は水平粘性係数, AV は鉛直粘性係数である. また球面座標系におけ
るラプラシアン演算子 (
![$\Dlapla[2]{}$](img19.gif) )は
)は
となる. さらに質量の保存は次のように表される. [1]
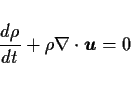 |
(2) |
ここに
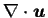 は次のように表される.
は次のように表される.
Takashi Kagimoto
1998-09-03
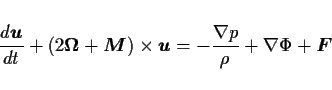
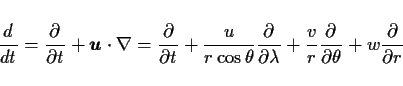

![\begin{displaymath}\Dlapla[2]{\phi} \equiv
\frac{1}{r^2\cos^2\theta}\DP[2]{\phi...
...\theta}\DP{}{\theta}
\left(\cos\theta\DP{\phi}{\theta}\right)
\end{displaymath}](img20.gif)
