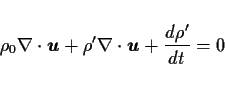

Next: β面近似
Up: スベルドラップ・バランス
Previous: 基礎方程式
海洋の密度は温度, 塩分, 圧力に依存する. 0bar (0m) において 35
psu[2], 25�Cの海水の密度は 1023.343
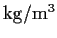 ,
600bar (約 6000m) において 35 psu, 2�Cの海水の密度は 1054.481
,
600bar (約 6000m) において 35 psu, 2�Cの海水の密度は 1054.481
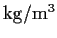 ,
であることから, 海水の密度はせいぜい 5% 程度しか変化しない.
そこで (2) 式において密度
,
であることから, 海水の密度はせいぜい 5% 程度しか変化しない.
そこで (2) 式において密度 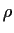 を
を
 とする(ただし
とする(ただし
 ).
).
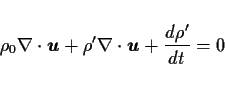 |
(3) |
海洋の運動において, 密度の時間および空間変化は一般に速度場の空間変化に比
べてはるかに小さいことが知られている. これは (3) 式第 3 項は第
2 項とほぼ同程度の大きさとなる. 第 1 項に比べると第 2 項ははるかに小さい
ので, 結局質量保存式は次のようになる.
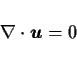 |
(4) |
同様に運動方程式 (1) においても 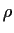 を
を 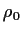 におきかえる.
ただし, 鉛直方向の運動方程式については重力加速度項のみ
におきかえる.
ただし, 鉛直方向の運動方程式については重力加速度項のみ 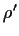 を残す.
これは浮力として働く重要な項だからである. 以上の近似を「ブジネスク近似」
と言う.
を残す.
これは浮力として働く重要な項だからである. 以上の近似を「ブジネスク近似」
と言う.
Takashi Kagimoto
1998-09-03