

Next: 方程式の無次元化
Up: スベルドラップ・バランス
Previous: ブジネスク近似
緯度 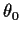 ,
経度
,
経度 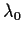 を原点として, その接平面上において東向
きを x, 北向きを y, 上向きを z とする局所デカルト座標に方程式系を
座標変換することを考える. 水平方向の微分は
を原点として, その接平面上において東向
きを x, 北向きを y, 上向きを z とする局所デカルト座標に方程式系を
座標変換することを考える. 水平方向の微分は
と変換される. また質量保存式の
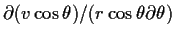 について考えると,
について考えると,
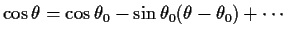 であるから,
であるから,
他のメトリック項も同様に座標変換すると, 結局次を得る.
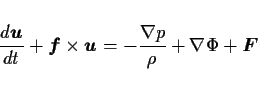 |
(5) |
ただし
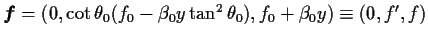 である. d/dt は次のように変換される.
である. d/dt は次のように変換される.
また
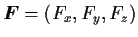 は
は
Takashi Kagimoto
1998-09-03
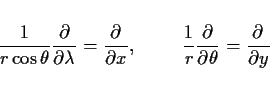
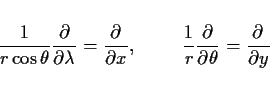
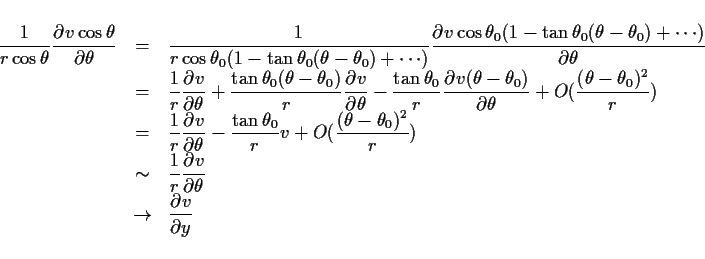
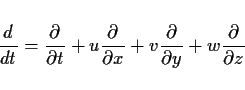
![\begin{displaymath}\begin{array}{rcl}
F_x & = & \Ddsty{ A_M \left(\DP[2]{u}{x} ...
...]{w}{x} + \DP[2]{w}{y}\right)
+ A_V \DP[2]{w}{z} }
\end{array}\end{displaymath}](img41.gif)