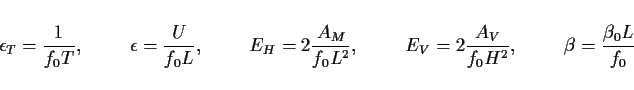

Next: 大洋スケールのバランス
Up: スベルドラップ・バランス
Previous: β面近似
運動の水平方向の空間スケールを L, 鉛直方向の空間スケールを H, 時間ス
ケールを T, 水平流速のスケールを U, 鉛直流速のスケールを W とする.
圧力に関しては平均密度 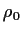 によって生じる圧力と, それからのずれとで
スケールをわけて, それぞれ P0, P とする. これらを用いてそれぞれの変
数を無次元化すると次のようになる.
によって生じる圧力と, それからのずれとで
スケールをわけて, それぞれ P0, P とする. これらを用いてそれぞれの変
数を無次元化すると次のようになる.
これらを (5), (4) 式に代入する. ただし簡略化のため無次
元であることを表す * は除く.
![\begin{displaymath}
\begin{array}{l} \Ddsty{
\frac{U}{T}\DP{u}{t}
+ \frac{U^2...
...t)
+ \frac{A_V U}{H^2}\left(\DP[2]{u}{z}\right) }
\end{array}\end{displaymath}](img43.gif) |
(6) |
![\begin{displaymath}
\begin{array}{l} \Ddsty{
\frac{U}{T}\DP{v}{t}
+ \frac{U^2...
...t)
+ \frac{A_V U}{H^2}\left(\DP[2]{v}{z}\right) }
\end{array}\end{displaymath}](img44.gif) |
(7) |
![\begin{displaymath}
\begin{array}{l} \Ddsty{
\frac{W}{T}\DP{w}{t}
+ \frac{UW}...
...t)
+ \frac{A_V W}{H^2}\left(\DP[2]{w}{z}\right) }
\end{array}\end{displaymath}](img45.gif) |
(8) |
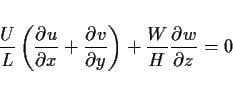 |
(9) |
(9) 式において
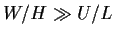 であるとすると, w は鉛直方向に一
定であることになる. もし w が有限な値を持っていた場合には, どこかの海
底付近において w を補うだけの水平収斂あるいは水平発散がなくてはならな
いが, 条件より u,v の収斂・発散は無視できるくらい小さいため, w を補
うだけの収斂・発散が生じ得ない. したがってこの条件は棄却される.
であるとすると, w は鉛直方向に一
定であることになる. もし w が有限な値を持っていた場合には, どこかの海
底付近において w を補うだけの水平収斂あるいは水平発散がなくてはならな
いが, 条件より u,v の収斂・発散は無視できるくらい小さいため, w を補
うだけの収斂・発散が生じ得ない. したがってこの条件は棄却される.
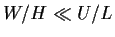 の場合には, u が収斂(発散)していた場合には v が発散(収斂)してそ
れを補えばよいので, 可能性のある条件である. また
の場合には, u が収斂(発散)していた場合には v が発散(収斂)してそ
れを補えばよいので, 可能性のある条件である. また
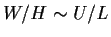 の場合に
は, 3 方向において収斂・発散がバランスしていることを意味している. したがっ
て,
の場合に
は, 3 方向において収斂・発散がバランスしていることを意味している. したがっ
て,
となる. ここで 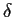 は鉛直スケールと水平スケールの比を表す無次元数で,
一般に大洋スケールの大循環を考える場合には 1 よりもはるかに小さい.
は鉛直スケールと水平スケールの比を表す無次元数で,
一般に大洋スケールの大循環を考える場合には 1 よりもはるかに小さい.
以後
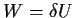 のバランスを考えて運動方程式 (6) 〜
(8) を見ることにする. (6) 〜 (8) 式の両辺を
f0U でわると次のようになる.
のバランスを考えて運動方程式 (6) 〜
(8) を見ることにする. (6) 〜 (8) 式の両辺を
f0U でわると次のようになる.
![\begin{displaymath}
\begin{array}{l} \Ddsty{
\epsilon_T\DP{u}{t}
+ \epsilon\l...
...right)
+ \frac{E_V}{2}\left(\DP[2]{u}{z}\right) }
\end{array}\end{displaymath}](img53.gif) |
(10) |
![\begin{displaymath}
\begin{array}{l} \Ddsty{
\epsilon_T\DP{v}{t}
+ \epsilon\l...
...right)
+ \frac{E_V}{2}\left(\DP[2]{v}{z}\right) }
\end{array}\end{displaymath}](img54.gif) |
(11) |
![\begin{displaymath}
\begin{array}{l} \Ddsty{
\delta\epsilon_T\DP{w}{t}
+ \del...
...
+ \delta\frac{E_V}{2}\left(\DP[2]{w}{z}\right) }
\end{array}\end{displaymath}](img55.gif) |
(12) |
ここで
となる.
Takashi Kagimoto
1998-09-03
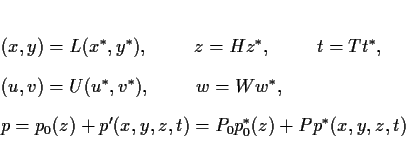
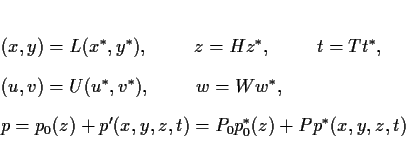
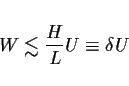
![]() のバランスを考えて運動方程式 (6) 〜
(8) を見ることにする. (6) 〜 (8) 式の両辺を
f0U でわると次のようになる.
のバランスを考えて運動方程式 (6) 〜
(8) を見ることにする. (6) 〜 (8) 式の両辺を
f0U でわると次のようになる.