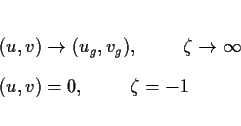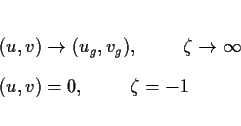

Next: スベルドラップ・バランス
Up: スベルドラップ・バランス
Previous: 海表面エクマン層
海底付近においても海底との摩擦によって粘性境界層が形成される. これを海底
エクマン層を呼ぶ. 方程式系は前節の海表面エクマン層と同様で
(20), (21) 式となる. ただし境界条件が次のように異なる.
ここで,
(ug, vg) は海底エクマン層付近の内部領域における地衡流で, 簡
単のため 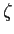 には依存しないことにする. この境界条件のもとで
(20), (21) を解くと次を得る.
には依存しないことにする. この境界条件のもとで
(20), (21) を解くと次を得る.
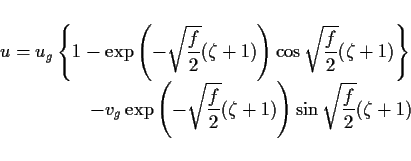 |
(32) |
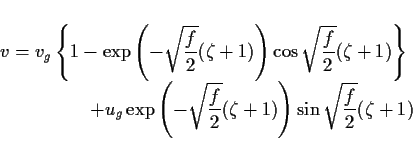 |
(33) |
これを図示すると図 2 のようになる.
Figure:
海底エクマン層におけるエクマン螺旋の概念図.
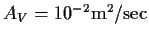 ,
,
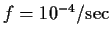 ,
,
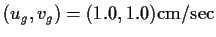 の 場合. 図のU 軸, V 軸の単位は
の 場合. 図のU 軸, V 軸の単位は
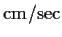 である.
である.
|
|
海底エクマン層内における非地衡流成分の質量輸送量を求めると,
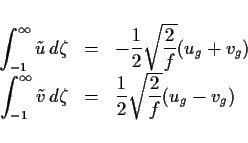 |
(34) |
質量輸送量の収斂は海底エクマン層上端における鉛直流速 -wB となることか
ら次を得る.
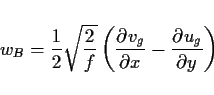 |
(35) |
ただし地衡流量の収斂は無視できるくらい小さいとした。
Takashi Kagimoto
1998-09-03